7.2. Classification Tutorial¶
7.2.1. 1. The data¶
Let’s look at a dataset used in one of the foundational papers in linear discriminant analysis (LDA) by Ronald Fisher. The data was actually collected by Edgar Anderson in a study of the morphological variation of iris species (variation due to shape).
First we load the data from the sklearn module, which contains many
tools and datasets used in machine learning research.
from sklearn.datasets import load_iris
data = load_iris()
features = data['data']
feature_names = data['feature_names']
target = data['target']
Two large arrays are defined, features and target.
The raw data about the irises is in features; features is a 2D
array.
features.shape
(150, 4)
That means we have 150 data exemplars (individual irises), and we have 4 measured attributes for each.
Here’s the first 10 rows
features[:10]
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
[ 4.4, 2.9, 1.4, 0.2],
[ 4.9, 3.1, 1.5, 0.1]])
To understand what the data means, consider an example iris. Let’s take the row 90 rows up from the end of the array.
P = features[-90]
P
array([ 5. , 2. , 3.5, 1. ])
Looking at feature names, we can decode this:
feature_names
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
P is an iris with sepal length 5 cm, sepal width 2 cm, petal length 3.5 cm, and petal width 1 cm. All of these are shape attributes.
P also has a class, stored in the target array, whose first ten
members are:
target[:10]
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
To find the class of our example iris, we look at the class of the iris 90 irises up from the last iris:
target[-90]
1
So P belongs to class 1. It turns out there are three classes, all numerical. We can see there are 3 classes and what they are by doing the following:
set(target)
{0, 1, 2}
Each number represents a different species of iris, 0 = I. setosa, 1 = I. versicolor, and 2 = I. virginica. In fact our data has 50 exemplars of each of these 3 species. So what this data helps us study is variation in shape attributes among iris species.
7.2.2. 2. Plotting attributes¶
Let’s do a picture.
Look at the picture created by the code below and study it carefully.
Each of the 6 subplots features a pair of attributes. For example, we pick sepal length amd sepal width in the first subplot. We then represent each iris as a point out on the 2D xy plane, using the sepal length as the x coordinate and sepal width as the y-coordinate, and we color it according to its class. The 3 classes of iris are rendered as blue, green, and red points of different shapes. This is called a scatter plot. The idea is to see if irises of of the same class cluster together based on the attributes we’re looking at.
One more thing we’ve done is to distinguish the example point P discussed above, so that you can see how its representation changes from subplot to subplot. P is of class 1; points of class 1 are being drawn as filled in green circles, but P has been drawn much larger than the other green points.
%matplotlib inline
import pylab
import numpy as np
from matplotlib import pyplot as plt
# Let's make this a big figure, because there are multiple subplots
pylab.rcParams['figure.figsize'] = (12.0, 9.0)
markers, colors = ">ox", "rgb"
# Four columns, plot two at a time. We'll need the indices of the cols we're pairing.
pairs = [(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)]
for i,(x,y) in enumerate(pairs):
# 6 subplots in 2x3 configuration. Each subplot pairs two iris
# attributes we call x and y. Let's do subplot i+1 now.
plt.subplot(2,3,i+1)
# On this subplot we're doing 3 sets of points, each belonging to a different iris class
# with a different color and shape used to draw the points. To do the 3 sets, use a loop.
# To loop through 3 sequences at once, zip them together first
for cls,marker,clr in zip(range(3),markers,colors):
plt.scatter(features[target == cls,x], features[target == cls,y], marker=marker, c=clr)
# Let's draw our point P with attention-getting large SIZE.
p_features,p_cls = features[-90],target[-90]
marker,clr = markers[p_cls], colors[p_cls]
plt.scatter(p_features[x],p_features[y],marker=marker,c=clr,s=100)
# Done with P
# Label this subplot with the names of the two features being studied.
plt.xlabel(feature_names[x])
plt.ylabel(feature_names[y])
# To make it prettier, uncomment the following & remove ticks on the x and y axis.
#plt.xticks([])
#plt.yticks([])
plt.savefig('../iris_datasets_separations.png')
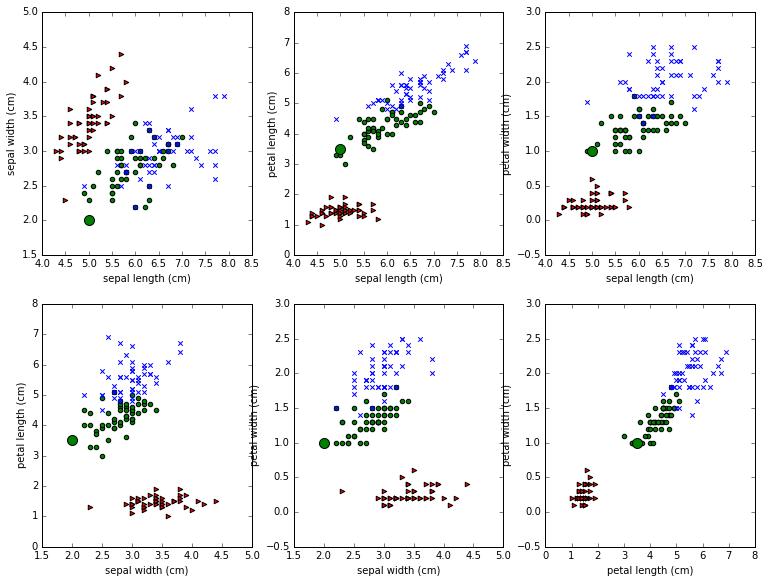
Notice that that big green dot P jumps around from plot to plot. It’s
being represented with different numerical values each time, so it jumps
around the xy-plane. In the first plot we see its sepal length/ sepal
width view, which happens to be the point (5,2). In the second plot we
look at the sepal length/petal length view, which happens to be the
point (5,3.5). Six different views as we scoot from subplot to subplot,
all coming from the one row in the features table that represent P:
[ 5. , 2. , 3.5, 1. ]
7.2.3. 3. Linear separation¶
Now consider the problem of drawing straight lines to separate the classes. First off it’s easy to see that it’s much easier to separate the red points from the blue and green points than it is to separate the blue points from the green points. As an example let’s draw a pretty good line for separating the red points from the others for the second plot in the first row. This is the one that plots sepal length (x-axis) against petal length (y axis). Note that I found the line by eyeballing the plot and using trial and error.
# After some trial & error, I decided a line specified by the following 2 numbers worked.
# m is the slope, b is where the line intercepts the y axis (not seen in the figure)
(m,b) = (.9,-2)
# The indexes for the two iris features we're using for this plot.
(p0,p1) = (0,2)
# Scatter the data points
for t,marker,c in zip(range(3),">ox","rgb"):
plt.scatter(features[target == t,p0], features[target == t,p1], marker=marker, c=c,s=60)
# Let's draw our point P with extra special attention getting large SIZE.
p_features,p_target = features[-90],target[-90]
marker,clr = ">ox"[p_target], "rgb"[p_target]
plt.scatter(p_features[p0],p_features[p1],marker=marker,c=clr,s=180)
# Draw our classifier line
# We'll only draw the portion of the line relevant to the current figure.
(xmin,xmax) = (3.,9.)
# tighten the boundaries on the drawing to the same limits
plt.gca().set_xlim(xmin,xmax)
#Between xmin and xmax, mark off a set of points on the x-axis .1 apart
xvec = np.arange(xmin,xmax,.1)
# Plot a stright line with the chosen slope & intercept
plt.plot(xvec,m*xvec+b)
plt.xlabel(feature_names[p0])
plt.ylabel(feature_names[p1])
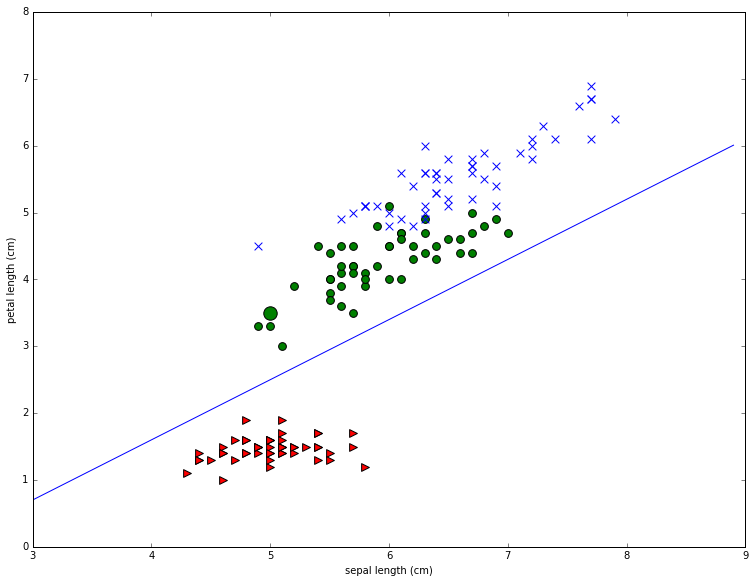
To see what this line does, consider our example iris P.
Let’s pretend we don’t know the class of P, but we do know its
attributes. So we know  has sepal length 5 and petal length
3.5.
has sepal length 5 and petal length
3.5.
Let’s plot it and use our line as a classifier.
pylab.rcParams['figure.figsize'] = (8.0, 6.0)
P = (5.0, 2., 3.5, 1.)
(xPrime,yPrime) = (P[0],P[2])
# Boundaries of what we'll draw.
(xmin,xmax) = (4.0,6.0)
# Ticks at which to place points on x- axis
xvec = np.arange(xmin,xmax,.1)
# our classifier line slope and intercept
(m,b) = (.9,-2)
# Use (m,b) for the EQUATION of the classifier line.
yvec = m*xvec+b
# Plot the classifier line
plt.plot(xvec,yvec)
# Plot our example point
plt.scatter(xPrime,yPrime , marker='o', c='g',s=60)
# Plot a point X below P, directly on the classifier line
plt.scatter([xPrime],[y] , marker='x', c='r',s=60)
xvec2,yvec2 =np.array([xPrime,xPrime]),np.array([y,yPrime])
# Plot the dashed line from X to P
plt.plot(xvec2,yvec2,linestyle='--')
# Draw the frame around the plots TIGHT
plt.axis('tight')
plt.xlabel(feature_names[p0])
plt.ylabel(feature_names[p1])
print y
2.5
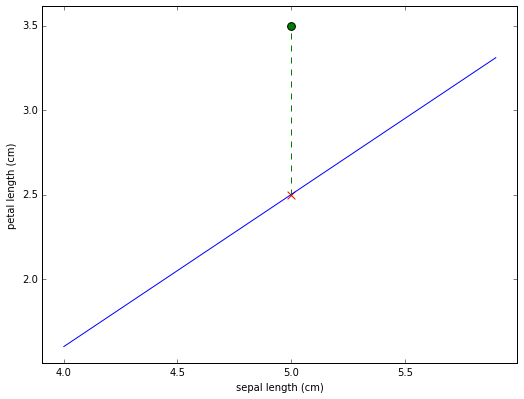
The representation of the iris 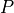 in this plotting system is
shown as the green dot. Since the dot falls above the line we would
classify it as a non-red class iris. Also shown (as a red X) is what the
petal length of
in this plotting system is
shown as the green dot. Since the dot falls above the line we would
classify it as a non-red class iris. Also shown (as a red X) is what the
petal length of 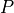 would have to be for it to fall directly on
the line.
would have to be for it to fall directly on
the line.
We printed out that value before drawing the plot. It’s 2.5. Basically for any iris with sepal length 5, if it’s petal length is greater than 2.5 we classify it as non-red; if it’s less than 2.5 we classify it as red. The line defines a classification rule.
Moreover we can easily extend the rule to any sepal length. In fact, we
can write a classification rule, using the equation for the line. Let
(x',y') be the point to classify, and let’s we call non-red the
positive class. Then we place (x',y') in the positive class
whenever the following quantity is positive (see the definition of
yvec in the code above):
y' - (.9x' - 2) = y' -.9x + 2
Taking our example point (x'=5,y'=3.5):
3.5 - .9*5 + 2 = +1
So as desired this is positive, telling us the point falls above the line and should be classified as non-red.
We have just created a classification rule. Next we write a function that implements our rule.
def is_non_red (P):
"""
P is a data point, all 4 attributes.
Return True if P is in positive class.
"""
return (P[2] - .9*P[0] + 2) > 0
P = features[-90]
print 'P is in positive class: {0}'.format(is_non_red(P))
P is in positive class: True
7.2.4. 4. Relationship to regression¶
How is what we’ve done related to regression, especially linear regression?
Well, first of all, in both the linear regression case and the linear discriminant case, we are using numerical data (a scattering of points) to try to determine a line.
We are defining the line in different ways. In the linear regression case, we looked for the best line to represent the scattering of points we saw. In the linear discrimination case, we are looking for the best line to separate two classes.
Just as it wasn’t always possible to find a line that was a good fit to our scattering of data, so it isn’t always possible separate a scattering of points with a line.
What we’re seeing in the plots above is that, taking the features by pairs, we can’t see a good way to separate all 3 classes.
We’ll validate this intuition in the next section. We’ll use a program that does a kind of linear discrimination; that is, it tries to find linear separations between classes. Instead of using Fisher’s method, which is called Linear Discriminant Analysis (LDA), we’ll use something called Logistic regression, which has become far more popular in many applications. The differences don’t matter for our purposes, but logistic regression is much more likely to be the method of choice in linguistic applications.
7.2.5. 5. Linear classifier results¶
We’re going to use sklearn to build a linear classifier to to
separate all three classes. We’re first going to use just the sepal
features, to keep it visualizable. We’ll use a type of linear classifier
called a Logistic Regression classifier.
from sklearn import linear_model
pylab.rcParams['figure.figsize'] = (12.0, 9.0)
X = features[:,:2]
Y = target
# we create an instance of a Logistic Regression Classifier.
logreg = linear_model.LogisticRegression(C=1e5)
# we fit the data.
logreg.fit(X, Y)
################################################################
# Dont worry too much about this part of the code. Meshes
# are a mesh-y topic
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = .02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
## End of meshy stuff xx,yy defines a mesh of points we're going to classify,
## So that we can color entire regions of the plot.
# Color the decision boundaries.
# Apply the classifier's decision function to xx,yy
# The result Z is an array storing a class for every point in xx,yy
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot. We'll color EACH point in xx,yy
# according to the value in Z.
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Also plot the training points, coloring them according to their TRUE classes.
for cls,marker,clr in zip(range(3),markers,colors):
plt.scatter(X[target == cls,0], X[target == cls,1], marker=marker, c=clr, s=50)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
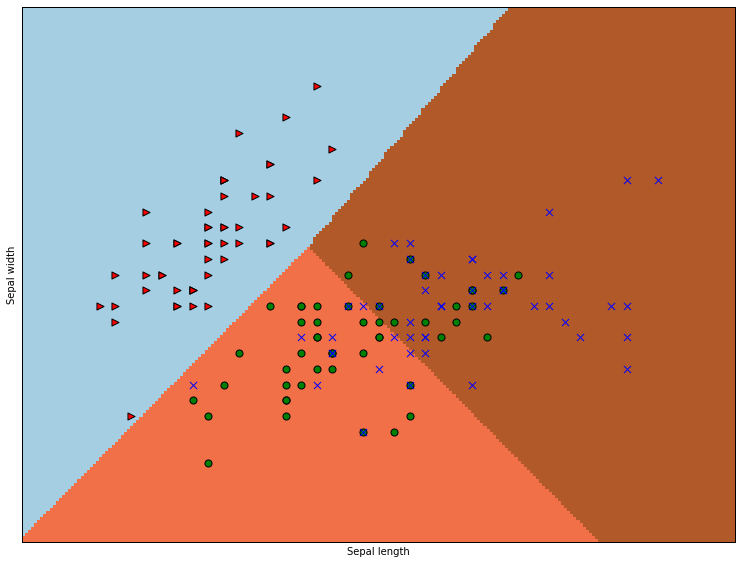
The differently colored regions represent the areas the classifier has reserved for particular classes, and the dots are colored as before. We see that all our worries about classes are validated. The classifier separates the red class off nicely, and has trouble discriminating the blue and green classes. Can we quantify what’s going on? Certainly.
Here’s how to find out our score.
from sklearn.metrics import accuracy_score
# Rerun prediction on just the training data.
logreg.fit(X, Y)
predicted = logreg.predict(X)
# Y has the right answers.
accuracy_score(Y,predicted)
0.80666666666666664
Well, we went and cheated by evaluating our score on just the training data, and we still didn’t do very well. Only 80% correct!
Maybe our problem is that we keep using only two features at a time. What if we use all the features at once? Please note how simple the following code is. We are basically starting from scratch, using all our data, and all our features, and testing.
X = features
Y = target
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X, Y)
predicted = logreg.predict(X)
accuracy_score(Y,predicted)
0.97999999999999998
Yep, that was our problem. Our accuracy is now 98%!
And so we pause for a moment to drink in one of the central lessons of multivariate statistics. Using more variables can help. Bigtime.
We started out essentially asking the question, what linear function of two of these variables can best separate these classes? And we tried all possible systems using two features and didn’t do very well. But then we switched to asking what linear function of all 4 variables can best separate these variables? And we did much better.
So why didn’t we do this to start with? And why did the code get so much simpler?
Second question, first, because the two answers are related. The code got much simpler because we threw out the visualization code. And we threw out the visualization code because we switched to a system that was much harder to visualize. We essentially went from representing our code in 2 dimensions (so that we could plot every point on an the xy plane) to representing it in 4 dimensions. Try and visualize 4 dimensions! Pretty hard. And that’s the answer to the first question. We didn’t do it this way to start with because we wanted something we could visualize, and that proved helpful, because there were insights the visualizations gave us, especially about the red class.
And therein lies one problem with switching to 4 dimensions. We’ve lost our capacity to glean insights from the data, at least with the tools we’ve looked at till now. We don’t really know what relationships got us over the hump in classifying irises.
So lesson number one is that more variables can help. And lesson number two is that there are perils involved in using more variables. Actually we haven’t even scratched the surface of the many perils involved in higher-dimensional data, but we’ve identified an important one. Using more variables makes things more complicated, and that makes it harder to understand what’s going on. At some point we are going to have turn around and explain our results to an audience waiting with baited breath, and you have be very careful when explaining multivariate results. Visualization is a big help at explaining complicated relationships, so losing the ability to visualize is not a small loss, especially since what real life problems often involve is not yes/no classifications, but insight. More on the problem of visualizing higher-dimensional data later in the course.
In the meantime, to try to recover a little insight into what is going on with a completely visualizable representation of the iris data, have a look at the appendix.
7.2.6. Homework¶
Don’t take my word for it that subsets of these features always do worse. Try it out.
Change the selector array in the next cell and execute the code in the cell to try out your own favorite subsets of features. No subset of 2 or even 3 features performs as well as using all 4.
For example, using this selector
selector = np.array([True,True,False,True])
leaves out just the third feature. Here’s your challenge: Find the best 2-feature system (it performs almost as well as any 3-feature system), and the best 3-feature system. Hint for the 2-feature problem, if you want to get there more quickly. Look at our plots of two-feature systems above. Which one looks like it gives the best separation?
selector = np.array([True, True, True, False])
X = features[:,selector]
Y = target
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X, Y)
predicted = logreg.predict(X)
accuracy_score(Y,predicted)
None
Above we implemented a function called
is_non_redthat distinguishes class 0 from classes 1 and 2. Write some code to evaluate the accuracy of this function. Use the evaluation functionaccuracy_scoreas illustrated above, but note that you can’t just evaluate against the class arraytargetbecause that has three classes andis_non_redessentially works with two. You have to start by creating a different class array that only has two classes, matching the kind of resultsis_non_redproduces. The red class is 0, so you wantTruefor every class 1 or 2 iris, andFalsefor every class 0 iris.
Hint: Use the following function, which applies the function
is_non_red to every row of the array features
np.apply_along_axis(is_non_red, axis=1, arr= features)
Be sure to say what your final score means. Did you you do very well or very badly?
Using the
rock vs. minesdata set loaded in the next cell, draw a scatterplot of the points like the ones we did in Section 2 and 3 of this tutorial for the iris data. You will find the code in Section 3 will require the least modification. This data set tries to distinguish two classes, rocks and mines, based on sonar readings. Note, as the loading code indicates, this data has 60 features, which is a lot, so you should just pick one pair of features out and plot them. Crucially, you don’t need to plot all pairs (there are 1770 pairs), even though with 60 features, you are unlikely to have much success using just two.
When modifying the code to draw the picture, bear in mind you really only need to scatter the points. You are not being asked to draw a separation line, and you don’t need to draw our point P, because it doesn’t appear in this data. You should try to give the points belonging to the two classes different colors and shapes, as was done above.
import pandas as pd
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-"
"databases/undocumented/connectionist-bench/sonar/sonar.all-data")
#read rocks mines data
mine_df = pd.read_csv(target_url, header=None, prefix="V")
mine_features = mine_df.values
(samp_sz, num_feats) = mine_features.shape
print '{0} exemplars with {1} features'.format(samp_sz, num_feats)
# The last column contains the class data. Separate it from the others.
target = mine_features[:, 60]
# Everything else is a feature
mine_features = mine_features[:, :60]
(samp_sz, num_feats) = mine_features.shape
# Find the two classes we're trying to separate.
feat_set = list(set(target))
print '{0} classes: {1}'.format(len(feat_set), feat_set)
208 exemplars with 61 features
2 classes: ['R', 'M']
7.2.7. Appendix: Combining variables: Cheap non-linearity¶
The Heidelberg stat-center reports a very nice result obtained by combining the 2 petal features and the 2 sepal features by multiplication. We end up with 2 area features, and a system that’s almost as good as a 4-feature linear system, at the cost of a little non-linearity (the multiplication). Here’s the computation, and the picture, both of which are very simple. Basically we see that petal area alone is enough to almost perfectly perform the discrimination. And the insight can easily be made visual.
sepal_area = features[:,0] * features[:,1]
petal_area = features[:,2] * features[:,3]
for t,marker,c in zip(range(3),">ox","rgb"):
plt.scatter(sepal_area[target == t], petal_area[target == t], marker=marker, c=c,s=60)
# Let's draw our point P with extra special attention getting large SIZE.
p_sepal_area,p_petal_area,p_target = sepal_area[-90],petal_area[-90],target[-90]
marker,clr = ">ox"[p_target], "rgb"[p_target]
plt.scatter(p_sepal_area,p_petal_area,marker=marker,c=clr,s=180)
# Let;s draw some linear separators, horizontal lines in this case
plt.plot(np.arange(0.,40.),np.array([1.8]*40))
plt.plot(np.arange(0.,40.),np.array([7.4]*40))
plt.axis('tight')
plt.xlabel('sepal area')
plt.ylabel('petal area')
<matplotlib.text.Text at 0x12b630210>
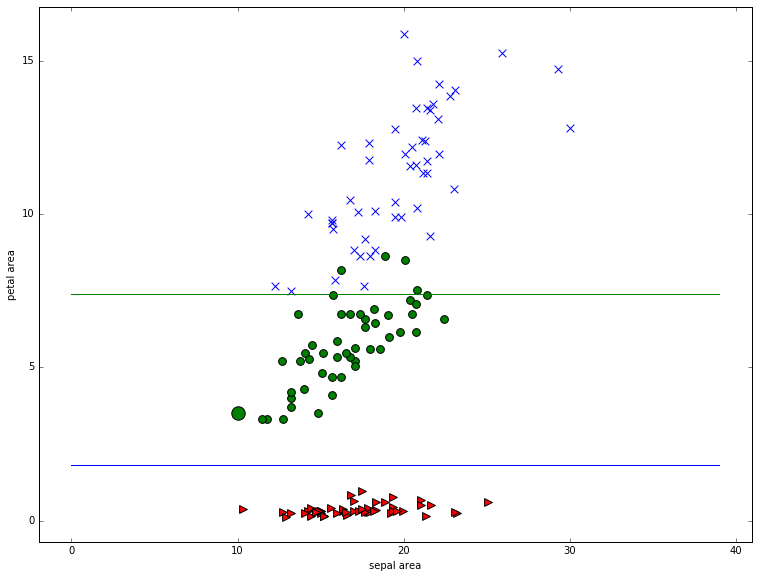
Our accuracy using just petal area os 96%!
X = np.array([petal_area]).T
Y = target
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X, Y)
predicted = logreg.predict(X)
accuracy_score(Y,predicted)
0.95999999999999996
And our accuracy using both area feature is 97.3%.
X = np.array([sepal_area, petal_area]).T
Y = target
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X, Y)
predicted = logreg.predict(X)
accuracy_score(Y,predicted)
0.97333333333333338
And actually using all the old features too helps us creep up toward 99%.
X = np.array([sepal_area, petal_area,features[:,0],features[:,1],
features[:,2],features[:,3]]).T
Y = target
logreg = linear_model.LogisticRegression(C=1e5)
logreg.fit(X, Y)
predicted = logreg.predict(X)
accuracy_score(Y,predicted)
0.98666666666666669
