Next: 5.3 Deriving scope ambiguities
Up: 5 Quantifiers
Previous: 5.1 A; Some
Contents
Index
We use 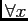 to mean ``for all x''
to mean ``for all x''
-
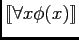 is true iff
for every x,
is true iff
for every x, 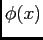 is true.
is true. 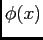 stands for
any formula that contains x.
stands for
any formula that contains x.
- So we need to look at a large number of cases;
Each needs to turn out true.
- How many cases? All of them. Every entity in the universe.
Translating English into logic can be difficult.
The meaning of the logic is rigorously defined and may not
always do what youy think it does:
- Every dog is a mammal.
-
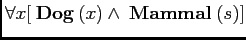
- This is the Wrong semantics.
- This requires every entity in the universe to be a dog
and every entity to be a mammal.
- Paraphrase: Everything is a dog and a mammal.
- We make no distinction between the truth condiutions
of every dog is a mammal (true) and Every mammal is a dog.
(false)
Right semantics
- Every dog is a mammal.
-
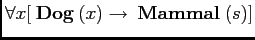
- This says of every entity in the universe:
if it's a dog, then it's a mammal.
- Paraphrase: Everything that is a dog is a mammal.
- Every mammal is a dog.
-
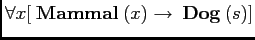 [different truth-conditions from (b)]
[different truth-conditions from (b)]
Combining every and
some
- Sentences which combine every and
some may be ambiguous!
- Every man loves some woman (Reading One)

- Every man loves some woman (Reading Two)

- Some woman loves every man. (Reading One)

- Some woman loves every man. (Reading Two)

Scope ambiguities: What are they?
- Lexical ambiguity
- John had all the good lines.
- Reading one: line is a short segment of dialogue in a play or performance
- Reading two: line is a length of cable or rope
- Scope ambiguities do not involve lexical ambiguity!
- Syntactic Ambiguity
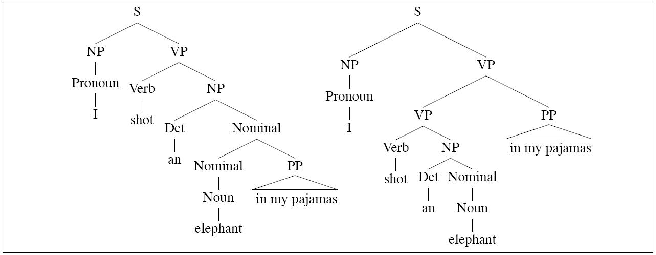
- I shot an elephant in my pajamas
- Reading one: I was in my pajamas at the time
- Reading two: ``How he got in pajamas I'll never know!'' (Groucho
Marx)
- Two trees
- Scope ambiguities do not involve syntactic ambiguity!





Next: 5.3 Deriving scope ambiguities
Up: 5 Quantifiers
Previous: 5.1 A; Some
Contents
Index
Jean Mark Gawron
2009-02-16
![]() to mean ``for all x''
to mean ``for all x''