9.3. Color¶
9.3.1. Using Colors and Color Maps I¶
9.3.1.1. 1. Parallel plots: Fisher’s irises¶
Load the fisher iris data.
%matplotlib inline
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plt
from sklearn import datasets
import matplotlib as mpl
import numpy as np
iris = datasets.load_iris()
X = iris.data[:,:4]
col_labels = iris.feature_names
df = pd.DataFrame(X, columns=col_labels)
Here are the attributes the sklearn data object has. The attributes
are common to many of the sklearn data sets.
iris.viewkeys()
Fisher’s data sets contains data on 3 species of iris.
iris.target_names
iris.target
iris.target is a 1D numpy array with the 3 targets assigned as ints
(0,1,2) and iris.data is a numpy array with the 4 attributes.
iris.feature_names
The data contains measurements for 4 morphological (shape-related) attributes of irises.
print iris.DESCR
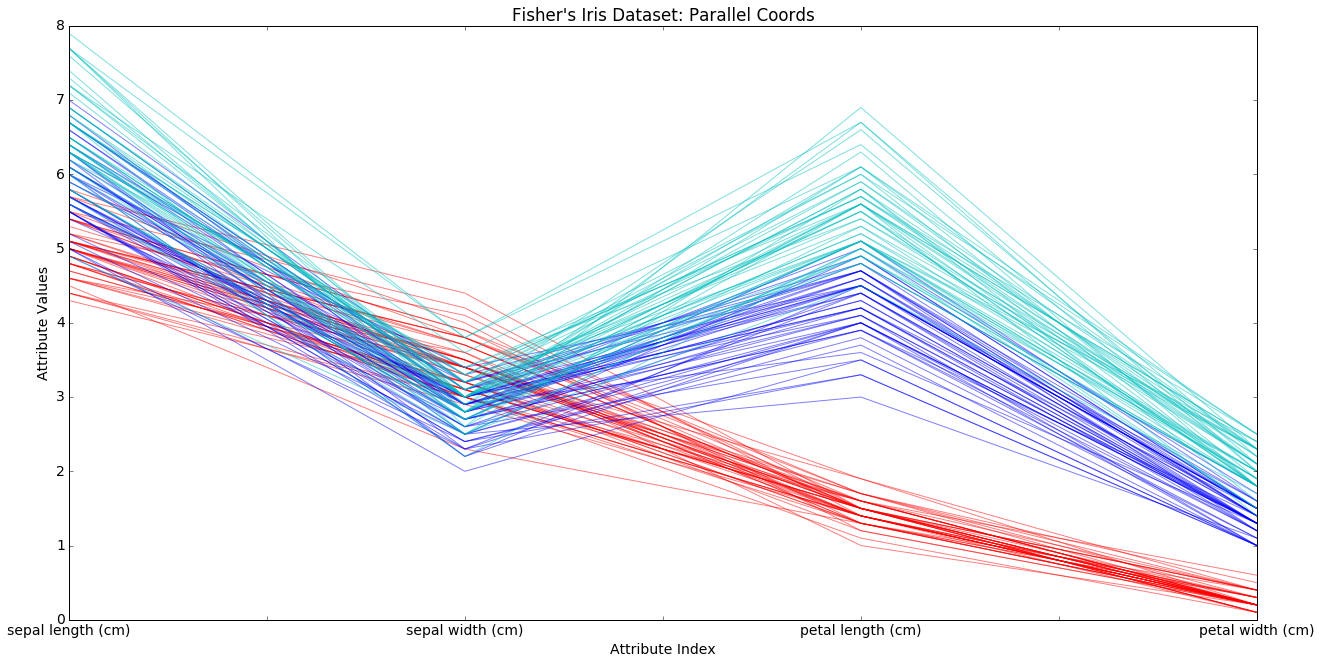
Next we draw what is known as a parallel coordinates plot of the data. See the reference section for more on such plots.
The x-axis is for the 4 morphological attributes, the y-axis for their values. We draw lines containing the values of the attributes for all data points, choosing the line color according to class. We first draw the line for one particular data point, iris 0, the first iris among our 150 exexamplar. By itself it tells us little.
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
#Choose a color
if iris.target[0] == 0:
pcolor = "r"
elif iris.target[0] == 1:
pcolor = "b"
elif iris.target[0] == 2:
pcolor = "c"
# identify the row to be plotted.
dataRow = df.iloc[0,:]
# `pandas` plot method uses matplotlib under the hood.
dataRow.plot(color=pcolor)
plt.title("One example iris")
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
## Draw
#plt.show()
<matplotlib.text.Text at 0x118828f10>

In the next cell we draw all 150 data lines. What we are doing is visualizing points in a 4-dimensional space.
We are looking for regularities within the classes, and there are some. We see condirable separation of the red class on the petal attributes, and a trend toward separation of the blue and green class on sepal attributes. But note there is considerable overlap as well. This is part of why those classes are harder to separate. Note also the the blue and greem classes move in parallel; they rise and fall together. This, together with the overlap, is why they are harder to separate.
Nevertheless, what we are seeing is consierable structure in the way the attributes are distributed. Compare the next example.
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
for i in range(len(X)):
#assign color based on Fisher's classes 0, 1 or 2
if iris.target[i] == 0:
pcolor = "r"
elif iris.target[i] == 1:
pcolor = "b"
elif iris.target[i] == 2:
pcolor = "c"
#plot rows of data as if they were series data
dataRow = df.iloc[i,:]
dataRow.plot(color=pcolor, alpha=0.5)
### Add some essentials to the plot before drawing
plt.title("Fisher's Iris Dataset: Parallel Coords")
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
## Draw
#plot.show()
<matplotlib.text.Text at 0x11890f550>
9.3.1.2. 2. Abalone parallel plots: Regression example (age prediction)¶
Adapted from code by Mike Bowles.
Fist load the abalone data. This is a regression problem, predicting a continuous value (age) from continuous independent variables.
import pandas as pd
import numpy as np
from pandas import DataFrame
import matplotlib as mpl
import matplotlib.pyplot as plot
from math import exp
target_url = ("http://archive.ics.uci.edu/ml/machine-"
"learning-databases/abalone/abalone.data")
#read abalone data
abalone = pd.read_csv(target_url,header=None, prefix="V")
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',
'Whole Wt', 'Shucked Wt',
'Viscera Wt', 'Shell Wt', 'Rings']
#get summary to use for scaling
summary = abalone.describe()
# We are going to use the max/min value for 'age' (number of rings
# to normalize ages)
minRings = summary.iloc[3,7]
maxRings = summary.iloc[7,7]
meanRings = summary.iloc[1,7]
sdRings = summary.iloc[2,7]
plt.clf()
<matplotlib.figure.Figure at 0x1188f6210>
The issue here is that since we are trying to predict age, so we don’t
have discrete classes to color. We’re using various weight and length
measurements to predict the age of the abalone, and using the number of
rings (stored in the target array) as our representation of age.
To color this data, then, we want a color map; a color map chooses from a range of colors based on a number it is given.
We’ll use a particular matplotlib color map called RdYlBu.
Here’s how it looks.
def draw_colormap (cmap_name,width=60,height=4,fontsize=50):
"""
cmap_name is a string.
"""
fig = plt.figure(figsize=(width,height))
ax = plt.gca()
mpl.rcParams['xtick.labelsize'] = fontsize
mpl.rcParams['font.size'] = fontsize
# Divide the interval from 0 to 1 into 256 parts.
gradient = np.linspace(0, 1, 256)
# The imshow function actually displays images,
# but you can pass it an array.
# In either case, the function wants 2D info.
# We give it an array with 2 rows,
# make the top half and bottom half of the image the same.
# We'll vertically stretch this very skinny image with aspect 'auto'.
# And the value of gradient will change the color value from left to right.
gradient = np.vstack((gradient, gradient))
ax.imshow(gradient, aspect='auto',cmap=plt.get_cmap(cmap_name))
# Show the number values associated with color on x-axis.
# The xvalues that imshow uses are pixel numbers, integers from 0 to 256.
ax.set_xticks(np.linspace(0,256,11))
# We'll label those with the inputs to the color map, numbers from 0 to 1
ax.set_xticklabels(np.linspace(0,1,11))
ax.set_yticklabels([])
# Put in an color map name you like here.
cmap_name = 'RdYlBu'
draw_colormap(cmap_name)

The RdYlBu color map wants numbers between 0 and 1 and will make
lower numbers in that range reddish, mid range number yellowish, and
higher numbers bluish, basically the range from hot to cool colors.
The cell below will draw a parallel plot for the abalone data using these color values. Patience. This may take a while.
The variable
labelColorin the code below is the normalized age of the abalone exemplar we’re drawing the line for. We pass this normalized age to our color map, which converts the age into a color. The yoiungest abalone should be red, the oldest blue, allthe others some color in between, where “in between” means according to the color map shown above. We see that the young (reddest) abalone are concentrated in the lower part of the plot, indicating, not surprisingly, that they have lower mesasurements on all the attributes.There are many different colormaps (see matplotlib colormaps demo). The
RdYlBumap is what’s called a divergent color map in thempldocs:These colormaps have a median value (usually light in color) and vary smoothly to two different color tones at high and low values. Diverging colormaps are ideal when your data has a median value that is significant (e.g. 0, such that positive and negative values are represented by different colors of the colormap).
Before mapping an age to a color the code below first normalizes the
age. We map the age to a number between 0 and 1 which represents what
proportion of the way this age is from the minimum age to the maximum
age. 3. We leave out non-numerical attributes. In this case, there’s
only 1, the Sex column.
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
for i in range(nrows):
dataRow = abalone.iloc[i,1:8]
# Getting the age info and "normalizing" it.
labelColor = (abalone.iloc[i,8] - minRings) / (maxRings - minRings)
# You can try this instead. It doesnt help much.
#labelColor = centered_age(abalone.iloc[i,8])
#Choose color for this line based on how old the exemplar is
dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)
#Use the dsame color for every exemplar. Dull.
#dataRow.plot(color=plot.cm.RdYlBu(.1), alpha=0.5)
plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
plot.show()
#renormalize using mean and standard variation, then compress
# with logit function
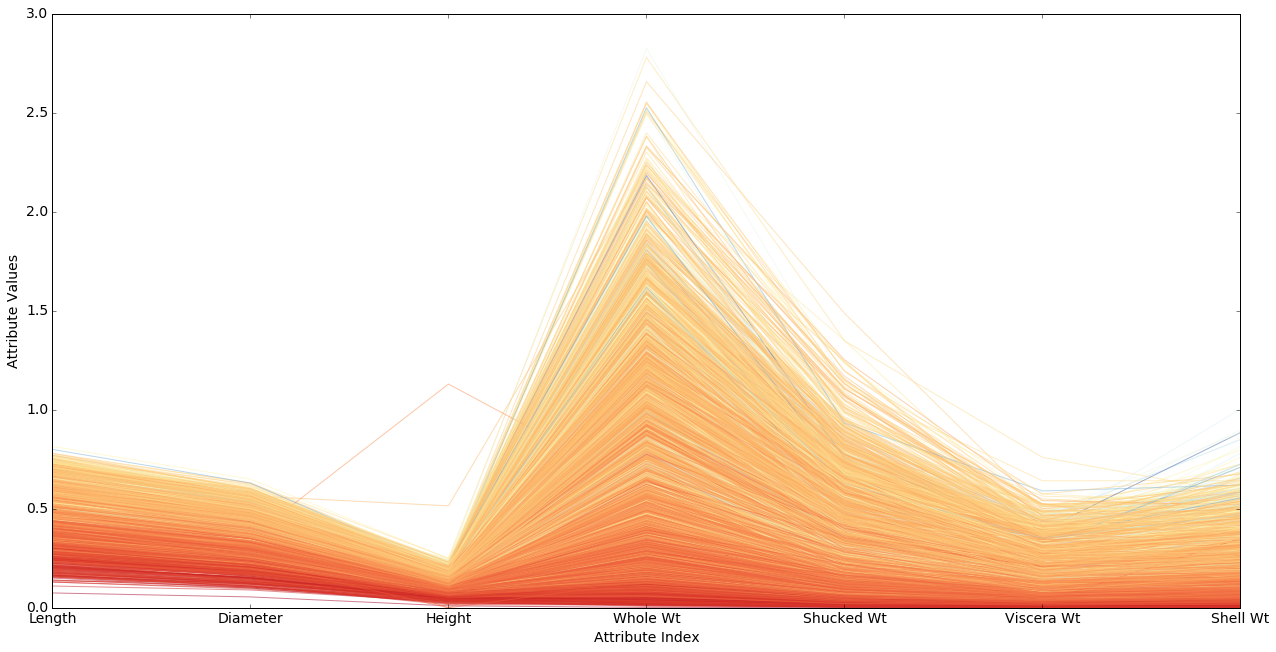
Note that almost all the colors fall in the red-yellow range. That means the right hand half of the color map shown in the cell above is almost entirely missing.
The problem is that our normalized data numbers don’t make very good use of the color map. The normalized age values go from about 0 to 1 as they should, but there are lots of abalone crowded into the reddish range and very few getting bluish colors. That means we’re wasting most of our color bandwidth.
What we need to do is recenter our data so that the most heavily populated part of the age range gets mapped to .5.
9.3.1.3. 3. Abalone data using inverse logit transform¶
So we do a very common data transformation. We do the logistic function,
or inverse-logit of the normalized ages:
$ x ({1 + e{-x}}){-1} $
This maps every centered age to a number between 0 and 1.
Note that we’re not going to change the values of the attributes in any way, just the way the plot lines are interpreted as colors. We’ll get the same overall silhouette for the plot.
def norm_age (x):
"""
This is what we were doing in the first plot.
"""
return (x - minRings) / (maxRings - minRings)
def centered_age (x):
"""
Here's the first step in the new mapping. Center the data.
Distance from mean divided by STD => distance above/below mean in
STD units.
"""
return (x - meanRings)/sdRings
def inverse_logit (x):
return 1./(1 + np.exp(-x))
Here are some numbers to give you an idea of what logit does to the
ages. The firat number is the age and the last number is the count of
the number of abalone exemplars of that age. In between are the
normalized ages and the inverse logit of the ages. The most heavily
populated part of the distribution is age 9 with a normalized value of
.29 and a logit value of .43, so that very popular age has been moved to
a value close to .5. So we get yellow for that age, and evenly balanced
blues and reds for the ages on either side.
from collections import Counter
# get the 9th column of the data, with the age info
ages = abalone.iloc[:,8]
(amax,amin) = ages.max(),ages.min()
# Keep track of how many exemplars there are of each age.
ctr = Counter(ages)
for i in range(amin,amax):
print '{0:>2} {1: .4f} => {2:.4f} {3:>3d}'.format(i, norm_age(i),inverse_logit(centered_age(i)),ctr[i])
1 0.0000 => 0.0589 1
2 0.0357 => 0.0787 1
3 0.0714 => 0.1043 15
4 0.1071 => 0.1370 57
5 0.1429 => 0.1780 115
6 0.1786 => 0.2279 259
7 0.2143 => 0.2870 391
8 0.2500 => 0.3544 568
9 0.2857 => 0.4281 689
10 0.3214 => 0.5051 634
11 0.3571 => 0.5819 487
12 0.3929 => 0.6550 267
13 0.4286 => 0.7213 203
14 0.4643 => 0.7792 126
15 0.5000 => 0.8280 103
16 0.5357 => 0.8678 67
17 0.5714 => 0.8995 58
18 0.6071 => 0.9243 42
19 0.6429 => 0.9433 32
20 0.6786 => 0.9578 26
21 0.7143 => 0.9687 14
22 0.7500 => 0.9769 6
23 0.7857 => 0.9829 9
24 0.8214 => 0.9874 2
25 0.8571 => 0.9907 1
26 0.8929 => 0.9932 1
27 0.9286 => 0.9950 2
28 0.9643 => 0.9963 0
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
# When experimenting with drawing params, draw only a subset of
# the rows, to reduce waittime
# nrows = 100
# Or set it back to what it should be
nrows = len(abalone.index)
for i in range(nrows):
dataRow = abalone.iloc[i,1:8]
# Center the data point
normTarget = (abalone.iloc[i,8] - meanRings)/sdRings
# Do inverse logit
labelColor = 1.0/(1.0 + exp(-normTarget))
dataRow.plot(color=plot.cm.RdYlBu(labelColor), alpha=0.5)
plot.xlabel("Attribute Index",fontsize=16)
plot.ylabel("Attribute Values",fontsize=16)
#plot.show()
<matplotlib.text.Text at 0x119c37a10>
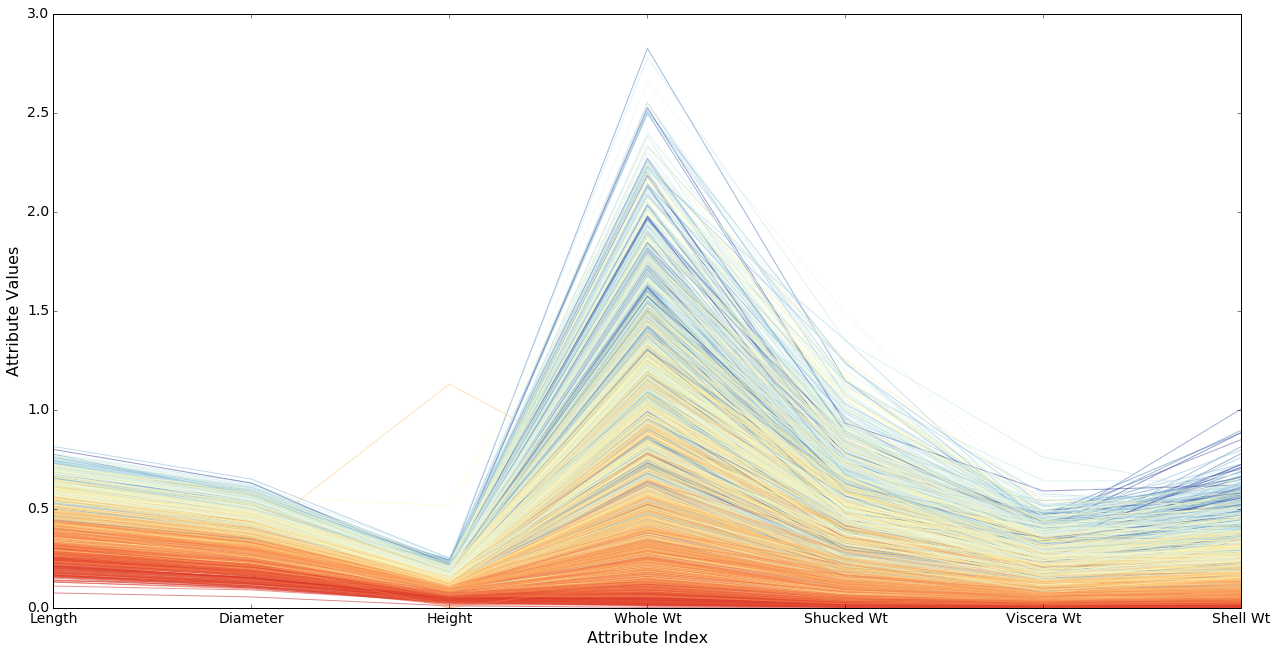
Now we can see the picture is considerable richer than it looked before. There are a large number of cases of older abalone with smaller than expected measurements (the darker stripes in various strata), and it looks as if those exemplars are consistently displaced. That is, if you have a smaller than average whole weight for your age, then you are likely to have a smaller than average height. If that’s true of all the attributes, the age of those exemplars is going to be hard to predict.
9.3.1.4. When it doesn’t work¶
Back to classification instead of regression.
Rock v. Mines data. 2 classes, two colors. Showing only 8 of 60 attributes below.
What goes wrong?
__author__ = 'mike_bowles'
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-"
"databases/undocumented/connectionist-bench/sonar/sonar.all-data")
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
#read rocks versus mines data into pandas data frame
rocksVMines = pd.read_csv(target_url,header=None, prefix="V")
<matplotlib.figure.Figure at 0x118849450>
print len(rocksVMines)
print rocksVMines.columns
# V60, the last column, is non-numerical; it's the one we're predicting
print set(rocksVMines.iloc[:,60].values)
208
Index([u'V0', u'V1', u'V2', u'V3', u'V4', u'V5', u'V6', u'V7', u'V8', u'V9',
u'V10', u'V11', u'V12', u'V13', u'V14', u'V15', u'V16', u'V17', u'V18',
u'V19', u'V20', u'V21', u'V22', u'V23', u'V24', u'V25', u'V26', u'V27',
u'V28', u'V29', u'V30', u'V31', u'V32', u'V33', u'V34', u'V35', u'V36',
u'V37', u'V38', u'V39', u'V40', u'V41', u'V42', u'V43', u'V44', u'V45',
u'V46', u'V47', u'V48', u'V49', u'V50', u'V51', u'V52', u'V53', u'V54',
u'V55', u'V56', u'V57', u'V58', u'V59', u'V60'],
dtype='object')
set(['R', 'M'])
Making use of the very useful pandas describe method on
dataframes, which prints out a number of statistics about the data.
summary = rocksVMines.describe()
rocksVMines.describe()
| V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V50 | V51 | V52 | V53 | V54 | V55 | V56 | V57 | V58 | V59 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | ... | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 | 208.000000 |
| mean | 0.029164 | 0.038437 | 0.043832 | 0.053892 | 0.075202 | 0.104570 | 0.121747 | 0.134799 | 0.178003 | 0.208259 | ... | 0.016069 | 0.013420 | 0.010709 | 0.010941 | 0.009290 | 0.008222 | 0.007820 | 0.007949 | 0.007941 | 0.006507 |
| std | 0.022991 | 0.032960 | 0.038428 | 0.046528 | 0.055552 | 0.059105 | 0.061788 | 0.085152 | 0.118387 | 0.134416 | ... | 0.012008 | 0.009634 | 0.007060 | 0.007301 | 0.007088 | 0.005736 | 0.005785 | 0.006470 | 0.006181 | 0.005031 |
| min | 0.001500 | 0.000600 | 0.001500 | 0.005800 | 0.006700 | 0.010200 | 0.003300 | 0.005500 | 0.007500 | 0.011300 | ... | 0.000000 | 0.000800 | 0.000500 | 0.001000 | 0.000600 | 0.000400 | 0.000300 | 0.000300 | 0.000100 | 0.000600 |
| 25% | 0.013350 | 0.016450 | 0.018950 | 0.024375 | 0.038050 | 0.067025 | 0.080900 | 0.080425 | 0.097025 | 0.111275 | ... | 0.008425 | 0.007275 | 0.005075 | 0.005375 | 0.004150 | 0.004400 | 0.003700 | 0.003600 | 0.003675 | 0.003100 |
| 50% | 0.022800 | 0.030800 | 0.034300 | 0.044050 | 0.062500 | 0.092150 | 0.106950 | 0.112100 | 0.152250 | 0.182400 | ... | 0.013900 | 0.011400 | 0.009550 | 0.009300 | 0.007500 | 0.006850 | 0.005950 | 0.005800 | 0.006400 | 0.005300 |
| 75% | 0.035550 | 0.047950 | 0.057950 | 0.064500 | 0.100275 | 0.134125 | 0.154000 | 0.169600 | 0.233425 | 0.268700 | ... | 0.020825 | 0.016725 | 0.014900 | 0.014500 | 0.012100 | 0.010575 | 0.010425 | 0.010350 | 0.010325 | 0.008525 |
| max | 0.137100 | 0.233900 | 0.305900 | 0.426400 | 0.401000 | 0.382300 | 0.372900 | 0.459000 | 0.682800 | 0.710600 | ... | 0.100400 | 0.070900 | 0.039000 | 0.035200 | 0.044700 | 0.039400 | 0.035500 | 0.044000 | 0.036400 | 0.043900 |
8 rows × 60 columns
Note that the summary object returned by rocksVMines.describe() is
itself a data frame, and can be used to find out a statistic about an
attribute. For example, to find out the mean of V3, do
summary.iloc[1,3]
0.053892307692307684
Note the maxes, means, stds, and medians rise steadily as we move
rightwards, but by the time we get to V50 they’re down again. Hmm.
It turns out this is sonar Time Series data, meaning we’re looking at data points taken from successive moments in time. The data is also cyclic, and it rises and falls, wavelike.
plt.figure(figsize=(20,10))
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
for i in range(208):
#assign color based on color based on "M" or "R" labels
if rocksVMines.iat[i,60] == "M":
pcolor = "red"
else:
pcolor = "blue"
#plot just 20 rows of data as if they were series data
dataRow = rocksVMines.iloc[i,0:8]
dataRow.plot(color=pcolor, alpha=0.5)
plot.xlabel("Attribute Index")
plot.ylabel(("Attribute Values"))
#plot.show()
<matplotlib.text.Text at 0x12affd6d0>
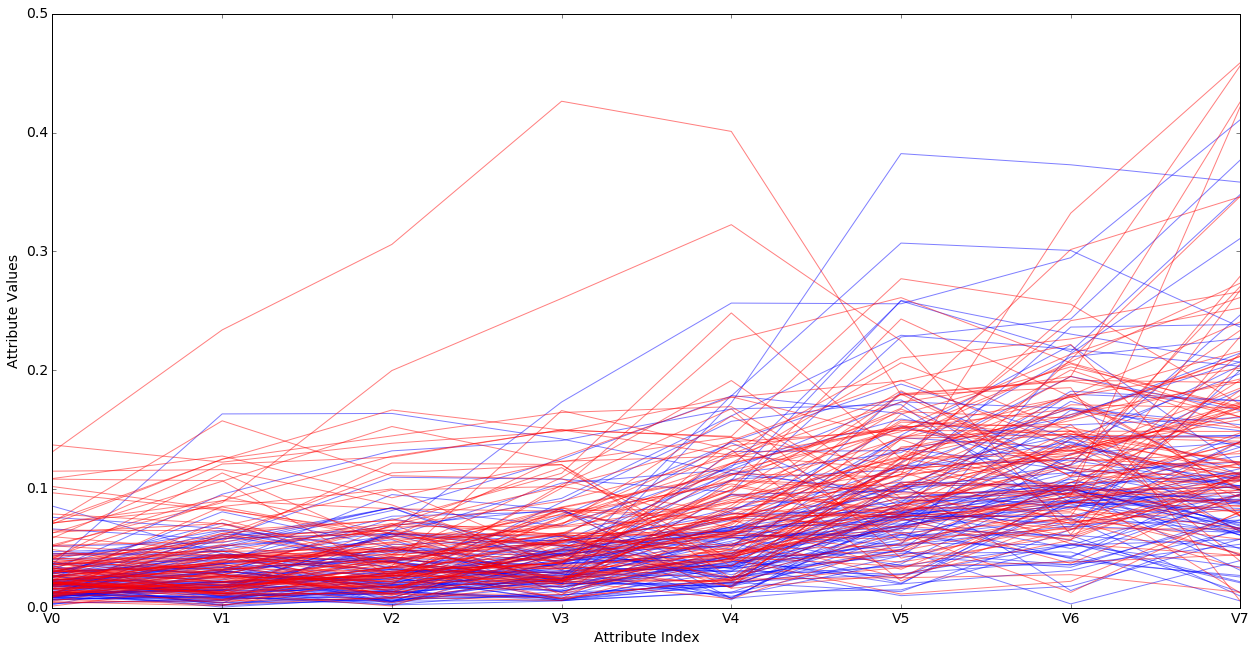
It looks as if there may be a tendency for very low values of most of the attributes to be rocks (blue), but there’s considerable mixing of the classes for many values and many attributes. In other words, it’s a mess.
9.3.1.5. Homework¶
Here is some wine data. The last column is what’s to be predicted, the quality. For some reason, the quality of the wine is represented as an integer from 3 to 8, with an average value of 5.6. So bad wine gets a score of 3, and the best wine a score of 8.
target_url = ("http://archive.ics.uci.edu/ml/machine-"
"learning-databases/wine-quality/winequality-red.csv")
wine = pd.read_csv(target_url,header=0, sep=";")
#print column names in order to have the full versions
print(wine.columns)
#change column names to shorter ones to fit graph
wine.columns = ['fixAcid', 'volAcid', 'citAcid',
'resSugr', 'chlor', 'frSO2', 'totSO2',
'dens', 'pH', 'sulpha', 'alcohol', 'quality']
#generate statistical summaries
summary = wine.describe()
nrows = len(wine.index)
tasteCol = len(summary.columns)
meanTaste = summary.iloc[1,tasteCol - 1]
sdTaste = summary.iloc[2,tasteCol - 1]
nDataCol = len(wine.columns) -1
Index([u'fixed acidity', u'volatile acidity', u'citric acid',
u'residual sugar', u'chlorides', u'free sulfur dioxide',
u'total sulfur dioxide', u'density', u'pH', u'sulphates', u'alcohol',
u'quality'],
dtype='object')
wine.describe()
| fixAcid | volAcid | citAcid | resSugr | chlor | frSO2 | totSO2 | dens | pH | sulpha | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 |
| mean | 8.319637 | 0.527821 | 0.270976 | 2.538806 | 0.087467 | 15.874922 | 46.467792 | 0.996747 | 3.311113 | 0.658149 | 10.422983 | 5.636023 |
| std | 1.741096 | 0.179060 | 0.194801 | 1.409928 | 0.047065 | 10.460157 | 32.895324 | 0.001887 | 0.154386 | 0.169507 | 1.065668 | 0.807569 |
| min | 4.600000 | 0.120000 | 0.000000 | 0.900000 | 0.012000 | 1.000000 | 6.000000 | 0.990070 | 2.740000 | 0.330000 | 8.400000 | 3.000000 |
| 25% | 7.100000 | 0.390000 | 0.090000 | 1.900000 | 0.070000 | 7.000000 | 22.000000 | 0.995600 | 3.210000 | 0.550000 | 9.500000 | 5.000000 |
| 50% | 7.900000 | 0.520000 | 0.260000 | 2.200000 | 0.079000 | 14.000000 | 38.000000 | 0.996750 | 3.310000 | 0.620000 | 10.200000 | 6.000000 |
| 75% | 9.200000 | 0.640000 | 0.420000 | 2.600000 | 0.090000 | 21.000000 | 62.000000 | 0.997835 | 3.400000 | 0.730000 | 11.100000 | 6.000000 |
| max | 15.900000 | 1.580000 | 1.000000 | 15.500000 | 0.611000 | 72.000000 | 289.000000 | 1.003690 | 4.010000 | 2.000000 | 14.900000 | 8.000000 |
As you can see the various columns have huge variety in the means, so it
is helpful to center them all and put them in STD units. This means the
maximums in all the columns will all be of comparable size. The next
cell defines a copy of the wine data frame called wineNormalized in
which the values of all the attributes have all been centered.
wineNormalized = wine
ncols = len(wineNormalized.columns)
for i in range(ncols):
mean = summary.iloc[1, i]
sd = summary.iloc[2, i]
wineNormalized.iloc[:,i:(i + 1)] = \
(wineNormalized.iloc[:,i:(i + 1)] - mean) / sd
Your job is to do a parallel plot of the wine data. Use logit as in
the second abalone plot. You can try both wine and
wineNormalized, but do at least the latter.
9.3.1.6. References¶
Fisher,R.A. “The use of multiple measurements in taxonomic problems” Annual Eugenics, 7, Part II, 179-188 (1936); also in “Contributions to Mathematical Statistics” (John Wiley, NY, 1950).
Wegman, E. J. (1990) Hyperdimensional data analysis using parallel coordinates. Journal of the American Statistical Association 85, 664-675.
Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth edition. Springer
Wikipedia. 2016. Parallel coordinates. Wikipedia page
9.3.2. Color and color maps 2: Correlation heat maps¶
Load the iris data and define a variant of the draw_colormap
function from the previous section.
%matplotlib inline
import pandas as pd
import numpy as np
from pandas import DataFrame
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,:4]
col_labels = iris.feature_names
# Shorten the attribute names
col_labels = [c[:-5] for c in col_labels]
df = pd.DataFrame(X, columns=col_labels)
def draw_colormap (cmap_name,width=60,height=4,fontsize=50,fig = None, ax=None,
ticklabels_bd = (0,1), num_ticks =11):
"""
cmap_name is a string.
"""
if fig is None:
fig = plt.figure(figsize=(width,height))
if ax is None:
ax = plt.gca()
#mpl.rcParams['xtick.labelsize'] = fontsize
#mpl.rcParams['font.size'] = fontsize
# Divide the interval from 0 to 1 into 256 parts.
gradient = np.linspace(0, 1, 256)
# The imshow function actually displays images,
# but you can pass it an array.
# In either case, the function wants 2D info.
# We give it an array with 2 rows,
# make the top half and bottom half of the image the same.
# We'll vertically stretch this very skinny image with aspect 'auto'.
# And the value of gradient will change the color value from left to right.
gradient = np.vstack((gradient, gradient))
ax.imshow(gradient, aspect='auto',cmap=plt.get_cmap(cmap_name))
# Show the number values associated with color on x-axis.
# The xvalues that imshow uses are pixel numbers, integers from 0 to 256.
ax.set_xticks(np.linspace(0,256,num_ticks))
# We'll label those with the inputs to the color map, numbers from 0 to 1
ax.set_xticklabels(np.linspace(ticklabels_bd[0],ticklabels_bd[1],num_ticks))
ax.set_yticklabels([])
# Put in an color map name you like here.
cmap_name = 'coolwarm'
The cell above loads the by now familiar iris data set.
We do something new with it. We calculate the correlations among all the attributes, including the correlation of each attribute with itself.
#calculate correlations between real-valued attributes
corMat = df.corr()
corMat
| sepal length | sepal width | petal length | petal width | |
|---|---|---|---|---|
| sepal length | 1.000000 | -0.109369 | 0.871754 | 0.817954 |
| sepal width | -0.109369 | 1.000000 | -0.420516 | -0.356544 |
| petal length | 0.871754 | -0.420516 | 1.000000 | 0.962757 |
| petal width | 0.817954 | -0.356544 | 0.962757 | 1.000000 |
Take a moment to look at the table to make sure you understand it.
Correlation scores go from -1 to 1. Perfect correlation is 1. Perfect negative correlation is -1.
Look at petal length and petal width. They have a correlation of .962757. That’s very high. That means that whenever petal length goes up, petal width almost always goes up by a corresponding amount. Whenever petal length goes down, petal width almost always goes down by a corresponding amount. The two length attributes also have a fairly high correlation, .871754, and sepal length and petal width also have a fairly high correlation. .817954.
However, although length and width are correlated for petals, they are anticorrelated for sepals. They have a negative correlation of -.109369.
Notice the entries along the diagonal are all 1. The correlation of any attribute with itself is perfect, so it’s 1. Notice also that the table is symmetric. Each correlation not on the diagonal appears twice. So the entry in row 3, column 1 is the same as the entry in row 1, column 3. Verify that that’s true, and that it makes sense.
What does correlation mean? Well it means what we said. If you compare the petal lengths of iris A and iris B, and B has a higher petal length than A, than there is a very good chance that the petal width of B is also bigger than the petal width of A — by a corresponding amount. We will omit the formula and the definition of correlation here, but intuitively it means that the distance from the mean in STD units of B’s width is very close to the distance from the mean in STD units of A’s width.
Negative correlation of two attributes means that if A’s value for the first is larger than B’s value, then A’s value for the second will tend to be smaller.
Next we try to turn this all into colors. We’re going to use another divergent color map because we want to clearly distinguish the negative correlations from the positive correlations. This one is called coolwarm. Blue (cool) will means negative correlation; red (warm) positive correlation. The stronger the correlation (positive or negative, the stronger (more saturated) the color.
Now here’s the same information using color. This kind of plot is called a correlation heat map. Generally we use hot colors to represent strong correlation, ccol colors for negative correlation.
# Make the data frame into an array. Reverse direction of rows to make diagonal point right way.
corMat2 = corMat.values[::-1]
#corMat2 = corMat.values
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['font.size'] = 14
#pd.set_option('display.width',200)
fig, axes = plt.subplots(nrows=2,ncols=1,figsize=(20,10))
# Add intuitive labels to axes
ax0,ax1 = axes[0],axes[1]
ax0.set_xticks(np.linspace(.5,3.5,4))
ax0.set_xticklabels(col_labels)
ax0.set_yticks(np.linspace(.5,3.5,4))
ax0.set_yticklabels(col_labels[::-1],rotation=45)
#ax0.set_yticklabels(col_labels,rotation=45)
#visualize correlations using heatmap
ax0.pcolor(corMat2,cmap=cmap_name)
#fig.colorbar(ax0,ticks=np.linspace(0,1,11))
draw_colormap(cmap_name,fig=fig,ax=ax1,ticklabels_bd=(-1,1))
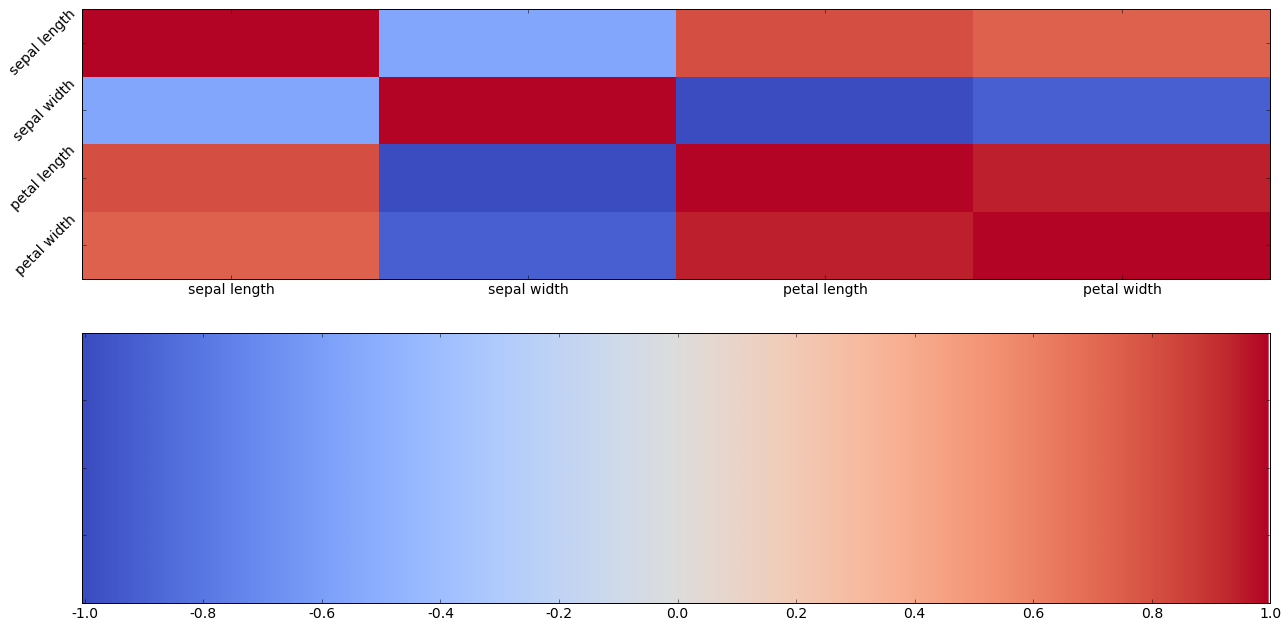
Using colors is nice but not that helpful here, because there are so few attributes. Let’s try using color with a larger array of attributes. In data mining mode, we might just be scanning a large square of color patches for patches patches of dark red.
target_url = ("http://archive.ics.uci.edu/ml/machine-"
"learning-databases/abalone/abalone.data")
abalone = pd.read_csv(target_url,header=None, prefix="V")
abalone.columns = ['Sex', 'Length', 'Diameter', 'Height',
'Whole weight', 'Shucked weight',
'Viscera weight', 'Shell weight', 'Rings']
col_labels = abalone.columns[1:]
#calculate correlation matrix excluding non numerical atribute 'Sex'
corMat = abalone.iloc[:,1:9].corr()
corMat2 = corMat.values[::-1]
#print correlation matrix
print(corMat)
summary = abalone.describe()
minRings = summary.iloc[3,7]
maxRings = summary.iloc[7,7]
nrows = len(abalone.index)
meanRings = summary.iloc[1,7]
sdRings = summary.iloc[2,7]
fig, axes = plt.subplots(nrows=1,ncols=1,figsize=(20,10))
ax0 = axes
ax0.set_xticks(np.linspace(.5,7.5,8))
ax0.set_xticklabels(col_labels)
ax0.set_yticks(np.linspace(.5,7.5,8))
ax0.set_yticklabels(col_labels[::-1],rotation=45)
#ax0.set_yticklabels(col_labels,rotation=45)
#visualize correlations using heatmap
plt.pcolor(corMat2,cmap=cmap_name)
#plot.show()
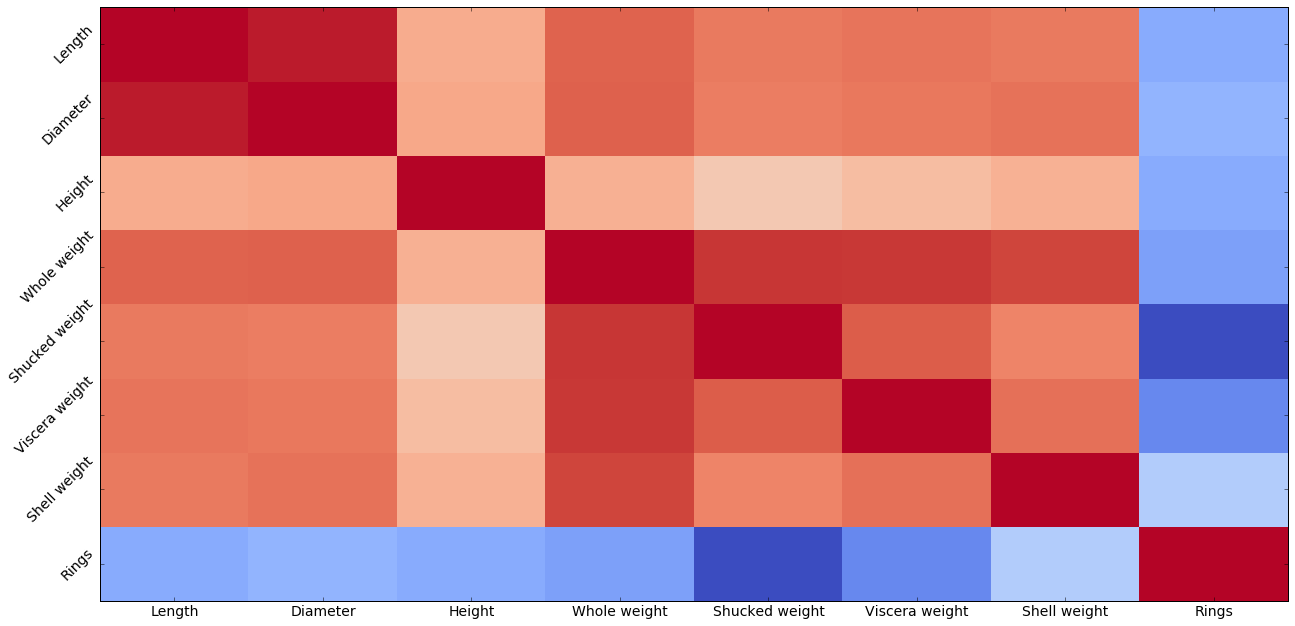
Looking down the last column is interesting, because it shows none of the attributes has a positive correlation with age.
9.3.2.1. Homework¶
Looking at the abalone correlation heat map, what has the strogest correlation with
Lengthother thanLength?What attribute has the strongest negative correlation with age. Does that mean it’s useless at predicting age? Explain why or why not.
What attribute has the strongest positive correlation with shell weight? Besides shell weight.
What pair of attributes comes the closest to “no relation” (= zero correlation)?
What is the numerical value of the correlation of shell weight with whole weight?
What is the numerical value of the correlation of shell weight with viscera weight?
Write some code that redraws the correlation heat map with the Rings column and row removed.
