9.1.1. Arrays for plotting¶
Note
Python and Ipython notebook versions of code
(.ipynb).
This section contains a very brief introduction to arrays, just enough to get you started on plotting.
As we noted in Section arrays, arrays are columns of numbers: contain items in sequence, like the following:
>>> import numpy as np
>>> x = np.array([1.0,2.,3.1])
Like lists you can access them by index:
>>> x[2]
3.1
As we noted when we first encountered arays, a fundamental
reason is space. We can save a great deal of space storing sequences if we know that all the items in the sequence are of the same data type. Another reason is time; mathematical operations can be made much more efficient if they are performed on sequences of uniform type. So the one-type restriction on arrays is quite helpful, in light of the fact that there are people out there doing massive amounts of number crunching involving very large arrays.
A large part of why arrays provide such massive gains in efficiency is vectorization of operations. To review, the fancy mathematical term for a column of numbers is a vector. To vectorize an operation means to generalize it from an operation on numbers to an operation on vectors. When you load numpy, vectorized versions of all the basic arithmetic operations are defined. For example, consider addition:
>>> x = np.array([1.0,2.,3.1])
>>> y = np.array([-1.0,-2.,2.9])
>>> x + y
array([ 0., 0., 6.])
The result of adding array x and array y is a new array whose $i$th element is the sum of $x[i]$ and $y[i]$.
Similar generalizations apply to all the 2-place arithmetic operations. So why should ordinary working data scientists care about arrays? One answer of course is that efficiency usually ends up mattering, even when you think it won’t. But there is a simpler answer that has immediate consequences even for beginners. Vectorization provides us with a lot of programming conveniences that make for clearer, more concise code. These benefits can be very nicely illustrated with plotting examples.
We now illustrate how vectorization works with user defined arithmetic functions:
def func(x):
return (x-3)*(x-5)*(x-7)+85
x = np.arange(0, 10, 0.01)
y = func(x)
Now y is an array containing the elementwise result of applying func to each element of x.
What all this has to do with plotting is this: The simplest
way to use pyplot is to give it two
columns of numbers as follows:
import matplotlib.pyplot as plt
plt.plot([1,2,3,4], [1,4,9,16], 'ro')
plt.axis([0, 6, 0, 20])
plt.show()
This plots the points (1,1), (2,4), (3,9), and (4,16).
So for each position 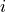 in arrays
in arrays 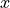 and
and 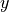 , we plot
(
, we plot
(![x[i]](../_images/math/77ed45ba10ba1d98a72398b21802def7a79b7717.png) ,
, ![y[i]](../_images/math/39cd64ca65ce2ff09fa934387c9ef90e0e09b987.png) ). This might seem a little
awkward at first, but the advantage becomes clear when
we use x as defined above:
). This might seem a little
awkward at first, but the advantage becomes clear when
we use x as defined above:
plt.plot(x, func(x), 'ro')
plt.axis([0, 10, 0, 20])
plt.show()
Remember that func(x) is an array containing the elementwise result of applying
func to each element of x. So for each position i in arrays x
and func(x), we plot the point (x[i],func(x[i])), which is just
what plotting a function should be.
The key point about arrays for now is this:
For many functions, applying a function $f$ to an array x returns an
array containing the results of applying $f$ elementwise
to x, so plotting $f$ over the interval given by x is
just a matter of giving plot the arguments f and f(x).
In particular, it is not quite true that arrays allow only things that are of one type. A single cell may also contain a structured tuple called a record. See this numpy page.
