4.6. Functions¶
This section contains examples motivating an important computing concept: functions.
Functions are named programs that take inputs and return results. The basic idea of a function is that it contains code that you want to reuse.
Consider one of our looping examples:
>>> rs = 'ABCDEFGHI'
>>> cs = '123456789'
>>> squares = []
>>> for row in rs:
for col in cs:
squares.append( row + col)
We are basically taking what is called the cross product of two sets: pair each member of the first set, with all the members of the second. The result is a list of strings that are two characters long:
['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'A9',
'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9',
'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9',
'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'D9',
'E1', 'E2', 'E3', 'E4', 'E5', 'E6', 'E7', 'E8', 'E9',
'F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8', 'F9',
'G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9',
'H1', 'H2', 'H3', 'H4', 'H5', 'H6', 'H7', 'H8', 'H9',
'I1', 'I2', 'I3', 'I4', 'I5', 'I6', 'I7', 'I8', 'I9']
This is something we might want to reuse so let’s name it and define it as follows:
def cross (rows, cols):
squares = []
for row in rows:
for col in cols:
squares.append( row + col)
return squares
Now we can use the function like this:
>>> rs = 'ABCDEFGHI'
>>> cs = '123456789'
>>> cross(rs, cs)
['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'A9',
'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9',
'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9',
'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'D9',
'E1', 'E2', 'E3', 'E4', 'E5', 'E6', 'E7', 'E8', 'E9',
'F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8', 'F9',
'G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9',
'H1', 'H2', 'H3', 'H4', 'H5', 'H6', 'H7', 'H8', 'H9',
'I1', 'I2', 'I3', 'I4', 'I5', 'I6', 'I7', 'I8', 'I9']
Several things are accomplished in the function definition:
We are writing a piece of code to do a particular task.
We are associating a name with it,
cross. The rules for function names are the same as the rules for variable names; that is, case matters, no digits in first position, no dollar signs or asterisks, and so on.We select the parameters of the function, the temporary variables whose values need to be set in order for the function to complete its computation. These are
rowsandcolsin the example. Notice how when we use the function,cross(rs,cs), it is followed by some expressions in parentheses. When the function is called (the technical term for “used”), the parametersrowsandcolsare set to be whatever it is applied to (the expressions in parentheses), in this casersandcs;rsandcsare called the arguments of the function. A function is reusable because it can be applied to a variety of arguments in a variety of contexts.Something is returned. An object we may to use in further computation.
Keeping in mind these four tasks will help both with defining functions and with using them. Thus, the first step in going from some lines of code to a function is to observe that this is a task you will want to do over and over:
>>> rs = 'ABCDEFGHI'
>>> cs = '123456789'
>>> squares = []
>>> for row in rs:
for col in cs:
squares.append( row + col)
The next step is to choose a name. The third and final task is to look
at the code lines and decide what names are being used within the code
that need to be defined
before the code-task can be completed. These will be the parameters
of the function. In this case the double loop uses three names:
rs, cs, and squares. But :squares
is the name of the list containing the result
of the computation. It does need to be defined
before the loop is executed, but it is created only for the purpose
of being used in the double loop. Thus, we define a function of two
parameters, making sure that squares is defined in the first
line of function code:
def cross (rows, cols):
squares = []
for row in rows:
for col in cols:
squares.append( row + col)
return squares
Note the last line, which uses the Python keyword return.
The return statement does not need to occur in the last
line of a function definition, but it frequently does. Whenever
Python encounters a return statement in the course
of executing a function, it immediately stops
executing the function and returns the value
of the expression that follows the return statement.
It is perfectly legal to define a function with no return
statement in it. In that case the function still returns
something when the block
of code completes its execution: the special Python object None.
Functions that return None are useful for a variety of purposes, for example,
user interactions, or some computation that changes the global
computational context. But for now we will focus on functions
that return a useful value. And that means we usually
set a variable to what the function returns. Thus we would usually
use cross as follows:
>>> my_squares = cross(rs, cs)
>>> my_squares
['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'A9',
'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'B9',
'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9',
'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'D9',
'E1', 'E2', 'E3', 'E4', 'E5', 'E6', 'E7', 'E8', 'E9',
'F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8', 'F9',
'G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9',
'H1', 'H2', 'H3', 'H4', 'H5', 'H6', 'H7', 'H8', 'H9',
'I1', 'I2', 'I3', 'I4', 'I5', 'I6', 'I7', 'I8', 'I9']
Now the list of squares is available for future use.
Now we have actually defined cross without using the
improvement we discussed when we introduced list
comprehensions:
rows = 'ABCDEFGHI'
cols = '123456789'
col_units = [r+c for r in rows for c in cols]
Modifying cross to use a list comprehension is quite simple, and makes it easier to read and understand:
def cross (rows, cols):
return [r+c for r in rows for c in cols]
This also illustrates how function definitions hide
complexity. There are different ways the same function could be written.
We can load a file that defines the function cross and call it to compute this
list of squares without ever reading its definition
or understanding exactly how it works. All we might care
about is that it computes the cross-product of two sequences.
4.6.1. Reasons for using functions¶
Here are three major reasons for using functions:
Reuse of code
Hiding unnecessary complexity
Making your code easier to understand
We’ve illustrated points 1 and 2. Now let’s illustrate point 3, using an example from the list comprehensions discussion.
Consider the code for creating all 9 box units in Sudoku puzzles, from that discussion:
box_units = [[l+n for l in lets for n in nums]
for lets in ('ABC','DEF','GHI')
for nums in ('123','456','789')]
Notice that the expression:
[l+n for l in lets for n in nums]
pairs each letter in lets with each numeral of nums. Since
there are 3 letters in each letter group, and three numerals
in each numeral group, this gives us
the 9 squares of a unit. This is
a fairly complicated operation all on its own and might well benefit
from being packaged up in a function definition.
Now notice that, exceopt for the the variable names, this is the same operation we just named
cross:
def cross (rows,cols):
return [r+c for r in rows for c in cols]
So we can rewrite the computation on box_units as follows:
box_units = [cross(lets,nums)
for lets in ('ABC','DEF','GHI')
for nums in ('123','456','789')]
Notice how much easier it is to understand. We know
what the operation cross, so we understand what this
code is doing: It takes the cross product of each of the
letter groups with each of the number groups, 9 cross
products in all, to make the set of box units. This is probably the
major reason for using function definitions. It makes
your program easier to to understand, especially if you give your
functions names that make it clear what they do.
4.6.2. Further examples¶
Python functions can of course compute mathematical functions. Some examples follow, to help illustrate the idea of reusability.
The formula for the area of a circle is:
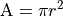
A function for computing the area of a circle:
from math import pi
def circle_area(r):
return pi * (r**2)
The formula for computing the volume of a sphere is:
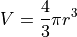
A function for computing the volume of a sphere:
from math import pi
def sphere_volume(r):
return (4.0/3) * pi * (r**3)
A slightly more efficient function for computing the volume of a sphere:
from math import pi
sphere_volume_constant = (4.0/3)*pi
def sphere_volume(r):
return sphere_volume_constant * (r**3)
The formula for computing the volume of a cylinder is:
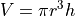
A function for computing the volume of a cylinder:
from math import pi
def cylinder_volume(r,h):
return pi * (r**2) * h
