7.1. Pandas Introduction¶
Pandas is Python’s most popular tool set for manipulating data in tabular form (Excel sheets, data tables). This section has two main goals. The first is to introduce the two main pandas data types, DataFrame and Series.
A DataFrame is a table of data. Datasets at all levels of analysis of analysis can be represented as DataFrames.
A DataFrame has values arranged in rows and column, like a 2D numpy array, but differing from it in two important respects:
Columns often contain data of some non-numerical type, especially strings. Distinct columns in the same DataFrame often contain distinct types. In numpy it’s useful to speak of the type of an array; in pandas, it’s more natural to speak of the type of a column.
A DataFrame uses keyword indexing instead of positional indexing.
Despite the change in how indexing works, all the principles that apply to computing with numpy arrays will carry over with minor modifications to computing with pandas DataFrames. This is especially true of Boolean indexing, which will be your fundamental tool for selecting and reshaping data in pandas. Where a DataFrame is like a 2D array, a Series is like a 1D array; both the rows and the columns of pandas DataFrames are Series objects.
The second goal of this section is to introduce you to some of pandas analytical tools, especially cross-tabulation and grouping,
By the end of the module, we will have covered using pandas for all of the following:
Create Data – We learn how to create pandas DataFrames from raw data in files or in Python containers.
Retrieve Existing Data - We will learn how to read in data from the web and other sources.
Analyze Data. We step though some simple analytical tasks with a number of different datasets, using pivot tables, cross-tabulation,. and grouping.
Present Data. We plot some data in graphs, mostly via the very helpful plotting facilities pandas offers, and peek under the hood a bit at the default pandas backend for plotting, matplotlib.
7.1.1. Create Data¶
Let’s start with a toy dataset, then we’ll ramp up.
The data set will consist of 5 baby names and the number of births recorded for a particular year (1880, as it happens).
# The initial set of baby names and birth rates
names = ['Bob','Jessica','Mary','John','Mel','Mel']
gender = ['M','F','F','M','M','F']
births = [968, 155, 77, 578, 973,45]
To merge these two lists together we will use the zip function.
BabyDataSet = list(zip(names,gender,births))
print(BabyDataSet)
[('Bob', 'M', 968), ('Jessica', 'F', 155), ('Mary', 'F', 77), ('John', 'M', 578), ('Mel', 'M', 973), ('Mel', 'F', 45)]
We next create a DataFrame.
df will be a DataFrame object. You can think of this object holding the contents of the BabyDataSet in a format similar to a sql table or an excel spreadsheet. Lets take a look below at the contents inside df.
df = DataFrame(data = BabyDataSet, columns=['Names', 'Gender', 'Births'],index = ['b','c','e','a','d','f'])
df
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| c | Jessica | F | 155 |
| e | Mary | F | 77 |
| a | John | M | 578 |
| d | Mel | M | 973 |
| f | Mel | F | 45 |
This pandas DataFrame consists of 6 rows and 3 columns. The
letters along the left edge are the index. The index provides names
or handles for the rows. The column names provide handles for the
columns.
One way to think of a DataFrame is as something like a numpy 2D
array which uses keyword indexing instead of positional indexing. Thus
instead of thinking of the item Mary as being in the row indexed by
2 and the column indexed by 0, we think of it as being in the row
indexed by e and the column indexed by Names.
7.1.2. Selecting Columns¶
To explore the idea of a DataFrame as a keyword-indexed 2D array,
let’s first look at a 1D object in pandas, a single column.
Columns in a pandas DataFrame are indexed by the column name:
names_col = df['Names']
names_col
b Bob
c Jessica
e Mary
a John
d Mel
f Mel
Name: Names, dtype: object
As the output shows, the row handles are part of the column object. so
the element Mary can be accessed by handle e.
names_col['e']
'Mary'
So a column is an object like a numpy 1D array, but indexed by
handles like b and e.
The data type of a column in pandas is Series.
type(df['Names'])
pandas.core.series.Series
The natural question to ask next is: Are rows also 1D objects in
pandas? And the answer is yes.
We demonstrate that next.
7.1.3. Selecting rows¶
The simplest way of selecting a pandas row is via the .loc
attribute:
Given a Dataframe and a row handle, df.loc[RowName] returns the row:
e_row = df.loc['e']
e_row
Names Mary
Gender F
Births 77
Name: e, dtype: object
As promised, this too is a Series.
type(e_row)
pandas.core.series.Series
Again it comes with handles for its elements. In this case those handles are column names:
e_row['Names']
'Mary'
The .loc method was needed to define e_row because the
df[keyword] syntax is reserved for the case where keyword is a
column name. Thus
# This produces a KeyError because 'e' is not a column name.
# df['e']
We’ve now seen two different ways to access the same DataFrame
element Mary:
df['Names']['e']
'Mary'
Call the syntax in the previous cell – Column handle first, then row handle – native pandas syntax. In this syntax, the DataFrame is like a dictionary whose keys are column handles, the columns are dictionaries whose keys are row handles.
We then introduced .loc.
df.loc['e']['Names']
'Mary'
Call the syntax with .loc[] numpy-like syntax. The idea is that
the syntax of .loc[] works like numpy with keyword indexing instead
of positional indexing. The numpy analogue of the syntax in the last
cell is
a = np.arange(12).reshape((3,4))
print(a)
r,c,val=2,3,11
print(f'{r=}, {c=} {val=}')
print(f'{a[r][c]=: 3d}')
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
r=2, c=3 val=11
a[r][c]= 11
The analogy can be pushed much further. Numpy also allows:
a[r,c]
11
Paralleling that in pandas, using .loc[], we have:
df.loc['e','Names']
'Mary'
Another similarity with numpy when we use .loc is that we can do
slicing.
Repeating df:
df
| Names | Births | |
|---|---|---|
| b | Bob | 968 |
| c | Jessica | 155 |
| e | Mary | 77 |
| a | John | 578 |
| d | Mel | 973 |
we take a row slice:
print(df.loc['c':'a'])
type(df.loc['c':'a'])
Names Births
c Jessica 155
e Mary 77
a John 578
pandas.core.frame.DataFrame
We get a sub-DataFrame starting up at row c, going up to and
including row e.
What’s a little surprising here is that we got 3 rows, where from all
our experience with normal Python slices, we would expect 2. This is not
a bug; the motivation is that we are not indexing by position, but by
the names of elements in the index. When you want to get a slice that
goes from row c to row a, all you have to know is those two
names; if we had to use the same convention used with slicing by
position, we would also have to know the name of the row following
a, which isn’t in general preductable.
As with numpy we can also slice along the column-axis.
df.loc[:,'Gender':'Births']
| Gender | Births | |
|---|---|---|
| b | M | 968 |
| c | F | 155 |
| e | F | 77 |
| a | M | 578 |
| d | M | 973 |
| f | F | 45 |
We can also do the pandas equivalent equivalent of fancy indexing in
numpy: Pass in a sequence or row handles to get a subset of the
rows:
df.loc[['b','c','f']]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| c | Jessica | F | 155 |
| f | Mel | F | 45 |
As with numpy the extra set of square brackets is required.
And of course we can do fancy-indexing with columns as well. The following command creates a new DataFrame omitting the gender column:
df.loc[:,['Names','Births']]
| Names | Births | |
|---|---|---|
| b | Bob | 968 |
| c | Jessica | 155 |
| e | Mary | 77 |
| a | John | 578 |
| d | Mel | 973 |
| f | Mel | 45 |
So we have indexing by keyword and two different ways of specifying it,
native-Pandas syntax and numpy-like using .loc[]. Does all this mean
positional indexing is completely abandoned in pandas?
No, as we will see, it’s possible, and it’s sometimes essential.
7.1.4. Boolean conditions¶
The most comon way of selecting rows is with a Boolean sequence.
For example, we can select the first, second and fifth rows directly as follows.
df[[True,True,False,False,True,False]]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| c | Jessica | F | 155 |
| d | Mel | M | 973 |
Or we can use a Boolean Series constructed from a Boolean condition on column values.
df[df['Names']=='Mel']
| Names | Gender | Births | |
|---|---|---|---|
| d | Mel | M | 973 |
| f | Mel | F | 45 |
This can also be written
df.loc[df['Names']=='Mel']
| Names | Gender | Births | |
|---|---|---|---|
| d | Mel | M | 973 |
| f | Mel | F | 45 |
We illustrate these constructions in the next few examples.
7.1.5. Selecting Rows with Boolean Conditions¶
Overview: The process of selecting rows by values involves two steps 1.
We use a Boolean conditions on a column (a 1D pandas Series object)
much as we did on numpy 1D arrays. The result is a
Boolean Series. 2. We use the Boolean Series as a mask to select a
set of rows, just as we did with arrays.
Placing a Boolean condition on a column works just as it did in numpy, The condition is applied elementwise to the elements in the colomn:
print(df['Births'])
print()
print(df['Births'] > 500)
0 968
1 155
2 77
3 578
4 973
Name: Births, dtype: int64
0 True
1 False
2 False
3 True
4 True
Name: Births, dtype: bool
The result is also a Series containing Boolean values.
type(df['Births'] > 500)
pandas.core.series.Series
Continuing the analogy with numpy: Just as we could use a 1D Boolean
array as Boolean mask to index a numpy 2D array, so we can use a pandas
Boolean Series to mask a pandas DataFrame.
df[df['Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
Given df[BS], where BS is a Boolean Series, pandas will
always try to align BS’s index with df’s index to do row
selection. That means BS must have the same row handles as df; a
mismatch raises an IndexingError.
For example, if we try to use only the first 4 rows of the
Boolean Series is the last example:
df[(df['Births'] > 500)[:4]]
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_4727/2043702469.py:1: UserWarning: Boolean Series key will be reindexed to match DataFrame index.
df[(df['Births'] > 500)[:4]]
---------------------------------------------------------------------------
IndexingError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_4727/2043702469.py in <module>
----> 1 df[(df['Births'] > 500)[:4]]
...
IndexingError: Unalignable boolean Series provided as indexer (index of the boolean Series and of the indexed object do not match).
df[BooleanSeries] is a synonym of df.loc[BooleanSeries]. Hence,
the expression in the next cell selects he same rows as the row
selection in the last example.
df.loc[df['Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
Notice that this expression has two indexing operations, one with
df.loc and one without. The inner one uses what we’ve been calling
native pandas like syntax, with a column specification in the square
brackets.
It’s possible to write this entirely in numpy-like syntax, but it gets
awkward. You would have to use exactly as many :s and ,s as
you do in selecting numpy rows:
df.loc[df.loc[:,'Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
This awkwardness is merely a consequence of having the .loc[] syntax
work like numpy: in each case, it has to be made clear whether rows
or columns are being selected.
That fussiness brings with it some flexibility. We saw above that the
.loc[] operator can be used to select columns with fancy-indexing.
It can also select them with a Boolean condition. To omit the Gender
column, we can do:
df.loc[:,[True,False,True]]
| Names | Births | |
|---|---|---|
| b | Bob | 968 |
| c | Jessica | 155 |
| e | Mary | 77 |
| a | John | 578 |
| d | Mel | 973 |
| f | Mel | 45 |
Or we can construct a Boolean Series containing the same Booleans using a condition on columns:
df.loc['a']!='M'
Names True
Gender False
Births True
Name: a, dtype: bool
What columns meet the condition that they don’t have the value M in
the a-row? The Names and Births columns. The Gender
column, on the other hand does have value M in the a-row, so its
Boolean value under this condition is False.
And using this condition as a column-selector, we again construct a
DataFrame lacking the gender column.
df.loc[:,df.loc['a']!='M']
| Names | Births | |
|---|---|---|
| b | Bob | 968 |
| c | Jessica | 155 |
| e | Mary | 77 |
| a | John | 578 |
| d | Mel | 973 |
| f | Mel | 45 |
As this example suggests, using Boolean conditions to select columns is less useful than using them to select rows. One can imagine situations where a Boolean condition might be the best way to select a set of columns, but they’re not all that common.
Since we will almost always be selecting rows with Boolean conditions we
can dispense with using the .loc[] syntax for Boolean conditions. So
rather than write:
df.loc[df.loc[:,'Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
we write
df[df['Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
or
df.loc[df['Births'] > 500]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| a | John | M | 578 |
| d | Mel | M | 973 |
Finally some comments on Boolean coditions and types. We note that
Boolean conditions on rows will always return a set of rows, which is
always a DataFrame.
Returning to our original example:
mel_rows = df[df['Names']=='Mel']
print(mel_rows)
print(type(mel_rows))
Names Gender Births
d Mel M 973
f Mel F 45
<class 'pandas.core.frame.DataFrame'>
We see that this Boolean condition happens to return a DataFrame
with two rows.
If the name is Mary there will just be one row, but what’s returned
will still be a DataFrame.
mary_rows = df[df['Names']=='Mary']
print(mary_rows)
print(type(mary_rows))
Names Gender Births
e Mary F 77
<class 'pandas.core.frame.DataFrame'>
Hence to get to, say, the numerical value for the number of babies with
the name Mary, we still need to select along two axes:
df[df['Names']=='Mary']['Births']['e']
77
7.1.6. Combining Conditions with Boolean operators¶
In numpy & is an operator that performs an elementwise and
on two Boolean arrays, producing a Boolean array that only has True
wherever both the input arrays have True.
import numpy as np
a = np.array([True,False,True])
b= np.array([False,True,True])
print('a', a)
print('b', b)
print('a & b', a&b)
a [ True False True]
b [False True True]
a & b [False False True]
Let B1 and B2 be two Boolean Series.
The & operator can also be used to combine two Boolean Series
instances. The result is a single Boolean Series that finds the rows
that satisfy both conditions.
df
| Names | Births | |
|---|---|---|
| 0 | Bob | 968 |
| 1 | Jessica | 155 |
| 2 | Mary | 77 |
| 3 | John | 578 |
| 4 | Mel | 973 |
df[(df['Births'] > 500) & (df['Births'] < 900)]
| Names | Gender | Births | |
|---|---|---|---|
| a | John | M | 578 |
Note that the parentheses are needed here.
As with numpy arrays, Series may also be combined with “bitwise not”
(~) and “bitwise or” (|).
The names which were used over 500 times but not 578 times:
df[(df['Births'] > 500) & ~(df['Births'] == 578)]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| d | Mel | M | 973 |
Applying the condition that the value in the Births column does not
fall between 500 and 900, we exclude the "John" row.
df[(df['Births'] < 500) | (df['Births'] > 900)]
| Names | Gender | Births | |
|---|---|---|---|
| b | Bob | M | 968 |
| c | Jessica | F | 155 |
| e | Mary | F | 77 |
| d | Mel | M | 973 |
| f | Mel | F | 45 |
7.1.7. Keyword indexing and Alignment¶
We have been at pains to emphasize that DataFrames are like 2D arrays but with keyword indexing instead of position based indexing.
One of the consequences of this is that shape is not the decisive factor in determining when two dataFrames can be combined by an operation.
When two numpy arrays of incompatible shapes are combined, the
result is an error:
A = np.ones((2,2))
B = np.zeros((3,3))
# This is a Value Error
A + B
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_76047/1019460503.py in <module>
2 B = np.zeros((3,3))
3 # This is a Value Error
----> 4 A + B
ValueError: operands could not be broadcast together with shapes (2,2) (3,3)
We use an example of Jake Van der Plas’s to show the same is not true of
pandas DataFrames:
M = np.random.randint(0, 20, (2, 2))
A = pd.DataFrame(M,
columns=list('AB'))
A
| A | B | |
|---|---|---|
| 0 | 11 | 19 |
| 1 | 18 | 2 |
DataFrame A is 2x2.
M = np.random.randint(0, 10, (3, 3))
B = pd.DataFrame(M,
columns=list('ABC'))
B
| A | B | C | |
|---|---|---|---|
| 0 | 5 | 3 | 2 |
| 1 | 6 | 1 | 0 |
| 2 | 6 | 3 | 7 |
DataFrame B is 3x3.
Now we combine these seemingly incompatible matrices, A and B:
A+B
| A | B | C | |
|---|---|---|---|
| 0 | 16.0 | 22.0 | NaN |
| 1 | 24.0 | 3.0 | NaN |
| 2 | NaN | NaN | NaN |
Whereever one of the DataFrames was undefined for a column/row name, we
got a NaN. More importantly, wherever we had positions that were
defined in both DataFrames, we performed addition.
The usefulness of this emerges when we we try to merge data from two different sources, each of which may have gaps. if we have our row and index labeling aligned, we may still be able to partially unify the information.
What applies to operations on numbers applies equally well to operations
on strings. Consider df an df2.
df
| Names | Births | |
|---|---|---|
| 0 | Bob | 968 |
| 1 | Jessica | 155 |
| 2 | Mary | 77 |
| 3 | John | 578 |
| 4 | Mel | 973 |
df2
| Names | Births | |
|---|---|---|
| 0 | Bob | 968 |
| 3 | John | 578 |
| 4 | Mel | 973 |
The two DataFrames share column names and some index names; one column contains numbers, the other strings.
The + operation — call it addition — is defined on both strings and numbers and will apply to any columns that can be aligned; so examine the 0, 3, 4 rows in the output of the next cell. Note that both columns undergo addition in those rows, while the unshared rows are NaN’ed.
df2 + df
| Names | Births | |
|---|---|---|
| 0 | BobBob | 1936.0 |
| 1 | NaN | NaN |
| 2 | NaN | NaN |
| 3 | JohnJohn | 1156.0 |
| 4 | MelMel | 1946.0 |
This kind of behavior follows from being consistent about keyword indexing and from allowing elementwise operations when possible:
df['Names'] + 'x'
0 Bobx
1 Jessicax
2 Maryx
3 Johnx
4 Melx
Name: Names, dtype: object
7.1.7.1. Vectorized operations with string Series¶
It is worth pointing out that pandas also tries to allow the string analogue of vectorized functions (functions that can be applied elementwise to arrays) whenever possible. Typically, this requires invoking a “StringMethod” accessor on the Series instance.
For example, although df['Names'].lower() is an error, we can
acomplish what we’re after here, lowercasing every element in the
column, by first calling the .str method, then .lower().
The .str() method provides an accessor to string methods which will
apply elementwise:
df['Names'].str
<pandas.core.strings.accessor.StringMethods at 0x7ff488e432e8>
df['Names'].str.lower()
0 bob
1 jessica
2 mary
3 john
4 mel
Name: Names, dtype: object
We can also use Boolean conditions on strings elementwise to select rows:
df[df['Names'].str.startswith('M')]
| Names | Births | |
|---|---|---|
| 2 | Mary | 77 |
| 4 | Mel | 973 |
The following expression returns a Series of first elements, preserving the original indexing.
df['Names'].str[0]
0 B
1 J
2 M
3 J
4 M
Name: Names, dtype: object
NaNs will as usual give rise to more NaNs, so .str methods will be robust to data gaps.
(df + df2)['Names'].str[0]
0 B
1 NaN
2 NaN
3 J
4 M
Name: Names, dtype: object
So if we want to collect data on correlations between name gender and name first letters, we can do:
df['Gender'].unique()
array(['M', 'F'], dtype=object)
for g in df['Gender'].unique():
print(g)
print(df[df['Gender']==g]['Names'].str[0])
print()
M
b B
a J
d M
Name: Names, dtype: object
F
c J
e M
f M
Name: Names, dtype: object
7.1.8. Sorting and positional indexing¶
To find the most popular name or the baby name with the highest birth rate, we can do one of the following.
Sort the dataframe and select the top row
Use the max() attribute to find the maximum value
We illustrate these in turn.
Next we create a new DataFrame, sorting the rows according to values
in a particular column. This column is called by by argument of
the .sort_values() method.
# Method 1 (old pandas)
Sorted_df = df.sort_values('Births', ascending= False)
Sorted_df
| Names | Gender | Births | |
|---|---|---|---|
| d | Mel | M | 973 |
| b | Bob | M | 968 |
| a | John | M | 578 |
| c | Jessica | F | 155 |
| e | Mary | F | 77 |
| f | Mel | F | 45 |
Often we want to be able to find the highest ranked row of such witout knowing its handle, so we are in a situation where keyword-indexing is not what we want.
To get to the actual name that is the most popular one, we need
positional indexing (first row after the sort). Fortunately, pandas
orovides positional indexing with .iloc[], which has a syntax very
similar to .loc[].
Sorted_df.iloc[0]['Names']
'Mel'
Of course if all we were interested in was the count of the most popular name, we could do:
# Method 2:
df['Births'].max()
973
Note that although we can just as easily sort a column (Series) as a DataFrame, it will be more work to find the associated value in another column.
Illustrating:
print(df['Births'])
SortedBirths = df['Births'].sort_values(ascending=False)
print(SortedBirths)
0 968
1 155
2 77
3 578
4 973
Name: Births, dtype: int64
4 973
0 968
3 578
1 155
2 77
Name: Births, dtype: int64
Now to get the most popular name, we must retrieve the first element in the sorted index, and then we can use that index element to get the name:
print(SortedBirths.index[0])
df.loc[SortedBirths.index[0],'Names']
4
'Mel'
7.1.9. Loading Data: A more realistic example¶
yob1881.txt
looks like this:Mary,F,7065
Anna,F,2604
Emma,F,2003
Elizabeth,F,1939
Minnie,F,1746
The code cell below will build a names DataFrame similar to that of
our toy example, but much larger and with two new columns, "sex" and
"year".
import pandas as pd
years = list(range(1880,2011))
pieces = []
columns = ['name','sex','births']
url = 'https://raw.githubusercontent.com/gawron/'\
'python-for-social-science/master/pandas/names/'
for year in years:
path = f'{url}yob{year:d}.txt'
frame = pd.read_csv(path,names=columns)
frame['year'] = year
pieces.append(frame)
names = pd.concat(pieces, ignore_index=True)
We first build the list pieces in the for-loop; pieces is a
list of DataFrames. As we process each data file, we keep track of the
year by adding a 'year' column to the DataFrame. We then concatenate
that list into a single large frame called names, ignoring the
indexes in the old frames. We ignore the indexes because they will all
be number ranges starting with 0, and rather than have a large number of
rows indexed 1 (1 from each year), we renumber them all.
Think about why it’s hard to build the list pieces with a list
comprehension instead of the way it’s done in the above cell. Notice the
following doesn’t work. Python requires an expression as the first
component of a list comprehension. One reason for this is that list
comprehensions are supposed to improve readability. Complex sequences of
commands don’t do that, and the for-loop above is much more
understandable.
pieces = [f=pd.read_csv('names/yob{0:d}.txt'.format(year),names=columns);
f['year']=year; f
for year in years]
If you were successful the next cell should evaluate to True. Please
re-evaluate the next cell to check.
len(names) == 1_690_784
True
We now have a large DataFrame of approximately 1.7 million rows,
with a default (numerical) index:
names
| name | sex | births | year | |
|---|---|---|---|---|
| 0 | Mary | F | 7065 | 1880 |
| 1 | Anna | F | 2604 | 1880 |
| 2 | Emma | F | 2003 | 1880 |
| 3 | Elizabeth | F | 1939 | 1880 |
| 4 | Minnie | F | 1746 | 1880 |
| ... | ... | ... | ... | ... |
| 1690779 | Zymaire | M | 5 | 2010 |
| 1690780 | Zyonne | M | 5 | 2010 |
| 1690781 | Zyquarius | M | 5 | 2010 |
| 1690782 | Zyran | M | 5 | 2010 |
| 1690783 | Zzyzx | M | 5 | 2010 |
1690784 rows × 4 columns
The new DataFrame has 1,690,784 rows and 4 columns.
names.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1690784 entries, 0 to 1690783
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 name 1690784 non-null object
1 sex 1690784 non-null object
2 births 1690784 non-null int64
3 year 1690784 non-null int64
dtypes: int64(2), object(2)
memory usage: 51.6+ MB
7.1.10. Selection: Selecting parts of Pandas data frames¶
Having created a much larger Pandas DataFrame with babynames data, we return to selecting data.
names1881 = names[names['year'] == 1881]
names1881
| name | sex | births | year | |
|---|---|---|---|---|
| 2000 | Mary | F | 6919 | 1881 |
| 2001 | Anna | F | 2698 | 1881 |
| 2002 | Emma | F | 2034 | 1881 |
| 2003 | Elizabeth | F | 1852 | 1881 |
| 2004 | Margaret | F | 1658 | 1881 |
| ... | ... | ... | ... | ... |
| 3930 | Wiliam | M | 5 | 1881 |
| 3931 | Wilton | M | 5 | 1881 |
| 3932 | Wing | M | 5 | 1881 |
| 3933 | Wood | M | 5 | 1881 |
| 3934 | Wright | M | 5 | 1881 |
1935 rows × 4 columns
The first ten rows.
print(type(names1881[:10]))
names1881[:10]
<class 'pandas.core.frame.DataFrame'>
| name | sex | births | year | |
|---|---|---|---|---|
| 2000 | Mary | F | 6919 | 1881 |
| 2001 | Anna | F | 2698 | 1881 |
| 2002 | Emma | F | 2034 | 1881 |
| 2003 | Elizabeth | F | 1852 | 1881 |
| 2004 | Margaret | F | 1658 | 1881 |
| 2005 | Minnie | F | 1653 | 1881 |
| 2006 | Ida | F | 1439 | 1881 |
| 2007 | Annie | F | 1326 | 1881 |
| 2008 | Bertha | F | 1324 | 1881 |
| 2009 | Alice | F | 1308 | 1881 |
Note that index starts with 2000 because we have retrieved a subset of
the rows in the names data, preserving the indexing.
Retrieve the gender column, and display the last part.
names1881['sex'].tail()
3930 M
3931 M
3932 M
3933 M
3934 M
Name: sex, dtype: object
A Boolean test, returning a DataFrame that has one column, a column of Booleans.
This shows the 1881 names are gender sorted, with the female names occupying approximately the last half of the data.
print(type(names1881['sex']=='F'))
names1881['sex']=='F'
<class 'pandas.core.series.Series'>
2000 True
2001 True
2002 True
2003 True
2004 True
...
3930 False
3931 False
3932 False
3933 False
3934 False
Name: sex, Length: 1935, dtype: bool
Using the analogue of fancy-indexing in numpy arrays (a list of indices selects a list of rows), you can pick out a subdata frame with a subset of columns, using a list of column names:
print(type(names1881[['sex','births']]))
names1881[['sex','births']]
<class 'pandas.core.frame.DataFrame'>
| sex | births | |
|---|---|---|
| 2000 | F | 6919 |
| 2001 | F | 2698 |
| 2002 | F | 2034 |
| 2003 | F | 1852 |
| 2004 | F | 1658 |
| ... | ... | ... |
| 3930 | M | 5 |
| 3931 | M | 5 |
| 3932 | M | 5 |
| 3933 | M | 5 |
| 3934 | M | 5 |
1935 rows × 2 columns
The indexing conventions we observed in the toy example work here.
indexing a series with a valid index member yields the value at that position in the series:
names1881['sex'][2000]
'F'
That’s why a Series is referred to as an ordered set in the Pandas documentation. There are usually no duplicate names, as with dictionary keys, but there is also ordering.
We can do Boolean selection as with the toy example.
print(type(names1881['name']=='Lee'))
lee_rows = names1881[names1881['name']=='Lee']
print(type(lee_rows))
lee_rows
<class 'pandas.core.series.Series'>
<class 'pandas.core.frame.DataFrame'>
| name | sex | births | year | |
|---|---|---|---|---|
| 2258 | Lee | F | 39 | 1881 |
| 2981 | Lee | M | 342 | 1881 |
So lee_rows is a DataFrame containing only the rows for people
named “Lee”.
This example also shows why we shouldn’t use the name column to
index the data. There are names that occur in two rows, because they are
both male and female names.
You can also pick out a sub data frame with just the female names. We do
that and query the “sex” column to show we’ve got a female_rows
DataFrame with about half the data of the original DataFrame.
print(type(names1881['sex']=='F'))
female_rows1881 = names1881[names1881['sex']=='F']
print(type(female_rows1881))
female_rows1881.tail()
<class 'pandas.core.series.Series'>
<class 'pandas.core.frame.DataFrame'>
| name | sex | births | year | |
|---|---|---|---|---|
| 2933 | Tinie | F | 5 | 1881 |
| 2934 | Tiny | F | 5 | 1881 |
| 2935 | Vernon | F | 5 | 1881 |
| 2936 | Verona | F | 5 | 1881 |
| 2937 | Viney | F | 5 | 1881 |
Since there are no male rows in female_rows1881, this is an empty
DataFrame:
female_rows1881[female_rows1881['sex'] == 'M']
| name | sex | births |
|---|
len(female_rows1881)
938
len(names1881)
1935
7.1.11. Summary/Review: Selection & Indexing¶
# Example df for the summary below, lower-case for the index, upper-case for the col names
import pandas as pd
df = pd.DataFrame.from_dict(dict(a=[1,11,111],
b=[2,22,222],
c=[3,33,333],
aa=[1,11,111],
bb=[2,22,222],
cc=[3,33,333]),
orient='index', # the keyword labeled items are rows
columns=['A',"B","C"] # need to label the columns independently
)
df
| A | B | C | |
|---|---|---|---|
| a | 1 | 11 | 111 |
| b | 2 | 22 | 222 |
| c | 3 | 33 | 333 |
| aa | 1 | 11 | 111 |
| bb | 2 | 22 | 222 |
| cc | 3 | 33 | 333 |
Reviewing and summarizing the discussion above using this example
Selection |
Native Pandas |
Numpy-like |
|---|---|---|
row |
NA |
df.loc[‘c’] |
row slice |
NA |
df.loc[‘c’: ‘bb’] |
col |
df[‘A’] |
df.loc[:,‘A’] |
row, col |
df[‘A’][‘c’] |
df.loc[‘c’,‘A’] |
df.loc[‘c’][‘A’] |
||
bool series |
df[‘A’] == 2 |
Not used |
bool selection |
df[df[‘A’] == 2] |
df.loc[df[‘A’] == 2] |
row (position) |
NA |
df.iloc[2] |
col (position) |
NA |
df.iloc[:,2] |
fancy (cols) |
df[[‘A’,‘C’]] |
df.loc[:,[‘A’,‘C’]] |
fancy (rows) |
NA |
df.loc[[‘b’,‘bb’]] |
The following cell gives the results of all the selection expressions listed above:
print("\nDataFrame")
print(df)
print("\nrow selection numpylike df.loc['c']")
print(df.loc['c'])
print("\nrow slice numpylike df.loc['c': 'bb']")
print(df.loc['c': 'bb'])
print("\nrow col native pandas df['A']['c']")
print(df['A']['c'])
print("\nrow col numpylike df.loc['c']['A']")
print(df.loc['c']['A'])
print("\nbool series native pandas df['A'] == 2")
print(df['A'] == 2)
print("\nbool selection native pandas df[df['A'] == 2]")
print(df[df['A'] == 2])
print("\nbool selection numpy like df.loc[df['A'] == 2]")
print(df.loc[df['A'] == 2])
print("\nrow (position) df.iloc[2]")
print(df.iloc[2] )
print("\ncol (position) df.iloc[:,2]")
print(df.iloc[:,2])
print("\n fancy indxing cols native pandas df[['A','C']]")
print(df[['A','C']])
print("\n fancy indxing cols numpylike df.loc[:,['A','C']]")
print(df.loc[:,['A','C']])
print("\n fancy indxing row df.loc[['b','bb']")
print(df.loc[['b','bb']])
DataFrame
A B C
a 1 11 111
b 2 22 222
c 3 33 333
aa 1 11 111
bb 2 22 222
cc 3 33 333
row selection numpylike df.loc['c']
A 3
B 33
C 333
Name: c, dtype: int64
row slice numpylike df.loc['c': 'bb']
A B C
c 3 33 333
aa 1 11 111
bb 2 22 222
row col native pandas df['A']['c']
3
row col numpylike df.loc['c']['A']
3
bool series native pandas df['A'] == 2
a False
b True
c False
aa False
bb True
cc False
Name: A, dtype: bool
bool selection native pandas df[df['A'] == 2]
A B C
b 2 22 222
bb 2 22 222
bool selection numpy like df.loc[df['A'] == 2]
A B C
b 2 22 222
bb 2 22 222
row (position) df.iloc[2]
A 3
B 33
C 333
Name: c, dtype: int64
col (position) df.iloc[:,2]
a 111
b 222
c 333
aa 111
bb 222
cc 333
Name: C, dtype: int64
fancy indxing cols native pandas df[['A','C']]
A C
a 1 111
b 2 222
c 3 333
aa 1 111
bb 2 222
cc 3 333
fancy indxing cols numpylike df.loc[:,['A','C']]
A C
a 1 111
b 2 222
c 3 333
aa 1 111
bb 2 222
cc 3 333
fancy indxing row df.loc[['b','bb']
A B C
b 2 22 222
bb 2 22 222
7.1.12. The .value_counts( ) method¶
Suppose we want to learn the number of distinct male and female names.
The easiest way to get that information is by using the Series method
.value_counts(). If called by Series S, this method creates a
new Series vc indexed by the distinct values of S: the value for
each index element of vc is the count of how many times that index
element occurred in S.
names1881 = names[names['year']==1881]
names1881['sex'].value_counts()
M 997
F 938
Name: sex, dtype: int64
The sum of the value counts equals the number of rows in names1881:
names1881['sex'].value_counts().sum()
1935
It turns out Series have a plot method; applying that method to the value_counts Series, we get:
names1881['sex'].value_counts().plot(kind='bar',
width=.3,
title='1881: Number of Names by Gender')
<AxesSubplot:title={'center':'1881: Number of Names by Gender'}>
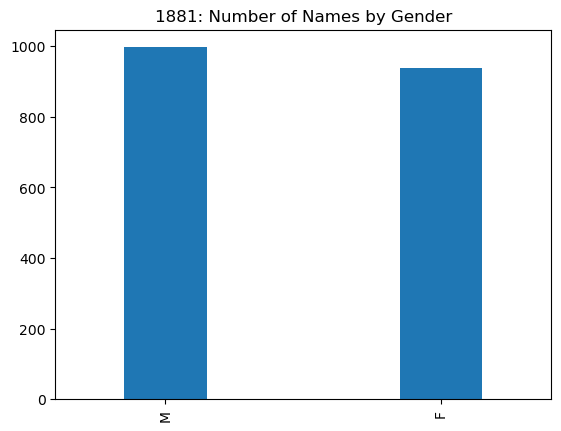
This is our first very simple example of analytical strategy we will use
often with pandas:
Use one of
pandasanalytical tools to transform the data into a new DataFrame or Series.Exploit the fact that the transformed data has restructured the index and the columns to make a plot summarizing our analysis.
The plot above shows there were fewer female names than male names in 1881. In fact,
female_names1881 = names1881[names1881['sex']=='F']
len(female_names1881)/len(names1881)
0.4847545219638243
only about 48.5% of the names in use were female.
Translating this code to the entire names data set (1881-2010), we
see an interesting change.
print(type(names['sex']=='F'))
female_names = names[names['sex']=='F']
len(female_names)/len(names)
<class 'pandas.core.series.Series'>
0.5937984982114806
names['sex'].value_counts().plot(kind='bar',width=.3,
title='1881--2007: Number of Names by Gender')
<AxesSubplot:title={'center':'1881--2007: Number of Names by Gender'}>
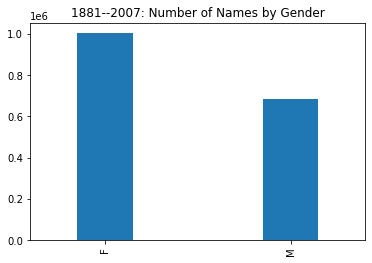
We see the female rows occupy nearly 60% of the data, meaning that some time after 1881 the diversity of female names overtook and greatly surpassed that of male names.
7.1.13. Cross-tabulation¶
To introduce cross-tabulation we will explore the fact we just discovered, that the proportion of female names increases over time
Before doing that, let’s try a simple exercise. If you already know how
to do cross-tabulation in pandas, feel free to use it. If you don’t
know how to do cross-tabulation in pandas, or perhaps what
cross-tabulation is, you should be able to do the problem using your
general knowledge of Python.
Plot the proportion of all names that were female names year by year to trace the year by year change.
Hint: create a sequence containing the numbers you need (proportion of
female names in each year). Then create a pandas DataFrame
female_names_by_year indexed by years with one column (‘Proportion
Female Names’). Then do
female_names_by_year.plot()
Note that for this exercise a line connecting the proportion values for each year, which is the default plot type (kind = “line”), is a better choice than a bar plot (kind = “bar”).
Optionally: Draw a horizontal line at 50% to help the viewer see where
the number of female names is greater than that of male names. The
births by year plotting example with matplotlib below may help,
since this involves some knowledge of matplotlib.
Two answers are provided several cells below.
They are not the only possible answers.
The answer is surprising. Female name diversity is not as simple as a continuously rising trend.
7.1.14. Solution 1¶
The following code is correct, and quite reasonable given what we’ve learned so far in this notebook but unnecessarily complicated. We show a simpler solution below which uses cross-tabulation.
Sine pandas provides some very flexible tools for making a
DataFrame from a dictionary, we start with a dictionary
comprehension that makes a dictionary with the data we want.
female_names = names[names['sex']=='F']
year_range = range(1881,2008)
def get_proportion_female_names(year):
# Given a year return the proportion female names that year
return (female_names['year'] == year).sum()/\
(names['year'] == year).sum()
# make a dictionary: year -> proportion of femal enames that year
result = {year: get_proportion_female_names(year) for year in year_range}
Making a DataFrame so we can use its plotting method.
# Dictionary to 1-column DF
# keys in dictionary will be used for the df index
female_names_by_year = \
pd.DataFrame.from_dict(result,
orient='index',
columns=['Proportion Female Names'])
female_names_by_year.plot()
<AxesSubplot:>
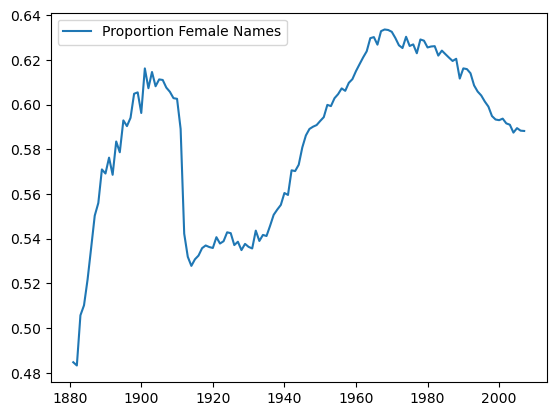
Here’s the DataFrame we used:
female_names_by_year[:5]
| Proportion Female Names | |
|---|---|
| 1881 | 0.484755 |
| 1882 | 0.483310 |
| 1883 | 0.505758 |
| 1884 | 0.510231 |
| 1885 | 0.521796 |
Second plot: Adding The 50% line. Note that we can get two lines just by
adding a second column to our female_names_by_year DataFrame.
# Creating axis for plot and secondary line, so a line can be added
from matplotlib import pyplot as plt
# Adding 50% line, using a vectorized assignment to populate
# a new column with a single value.
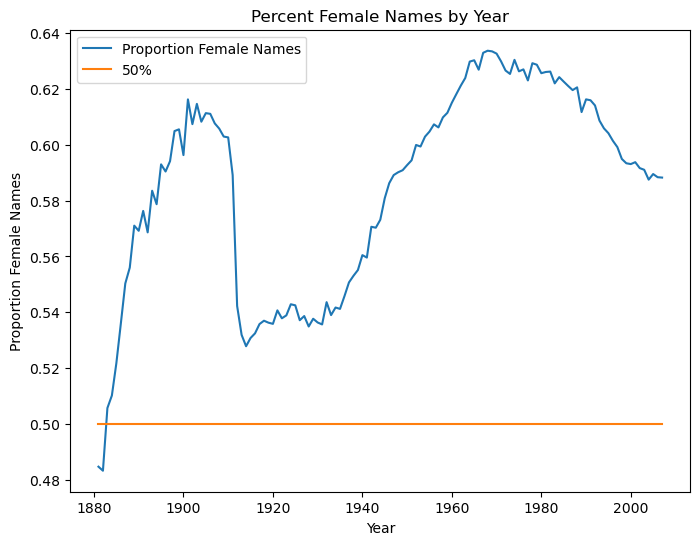
female_names_by_year['50%'] = .5
# Including axis labels, title
female_names_by_year.plot(xlabel='Year',ylabel='Proportion Female Names',
title='Percent Female Names by Year',
figsize=(8,6))
<AxesSubplot:title={'center':'Percent Female Names by Year'}, xlabel='Year', ylabel='Proportion Female Names'>
7.1.15. Solution 2¶
A much simpler solution, using the pandas crosstab function:
# This version gives percentages
gender_counts_by_year = pd.crosstab(names['sex'],names['year'],normalize='columns')
gender_counts_by_year
# This version would give us counts rather than percentages
# gender_counts_by_year = pd.crosstab(names['sex'],names['year'])
| year | 1880 | 1881 | 1882 | 1883 | 1884 | 1885 | 1886 | 1887 | 1888 | 1889 | ... | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sex | |||||||||||||||||||||
| F | 0.471 | 0.484755 | 0.48331 | 0.505758 | 0.510231 | 0.521796 | 0.535953 | 0.550358 | 0.556017 | 0.571042 | ... | 0.593765 | 0.591646 | 0.59104 | 0.587513 | 0.589516 | 0.588384 | 0.588252 | 0.583214 | 0.581556 | 0.582127 |
| M | 0.529 | 0.515245 | 0.51669 | 0.494242 | 0.489769 | 0.478204 | 0.464047 | 0.449642 | 0.443983 | 0.428958 | ... | 0.406235 | 0.408354 | 0.40896 | 0.412487 | 0.410484 | 0.411616 | 0.411748 | 0.416786 | 0.418444 | 0.417873 |
2 rows × 131 columns
Note that gender_counts_by_year is a DataFrame; the index is the
two genders.
It includes percentages (by column) because we passed crosstab the
parameter normalize="columns".
This means gender_counts_by_year.loc['F'] is a DataFrame row, that
is a Series whose index is the column sequence.
f_row = gender_counts_by_year.loc['F']
f_row
year
1880 0.471000
1881 0.484755
1882 0.483310
1883 0.505758
1884 0.510231
...
2006 0.588384
2007 0.588252
2008 0.583214
2009 0.581556
2010 0.582127
Name: F, Length: 131, dtype: float64
Since a Series has a plot method, we have the following simple option, which leaves out the 50% line.
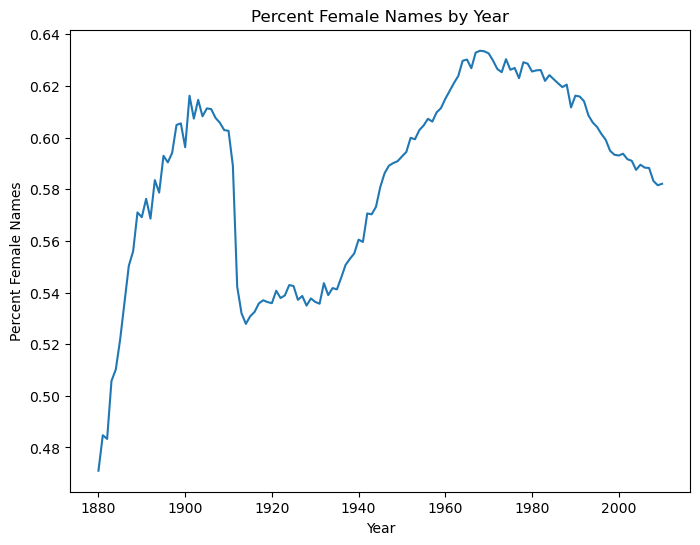
f_row.plot(ylabel='Percent Female Names',xlabel='Year',
title='Percent Female Names by Year', figsize=(8,6))
<AxesSubplot:title={'center':'Percent Female Names by Year'}, xlabel='Year', ylabel='Percent Female Names'>
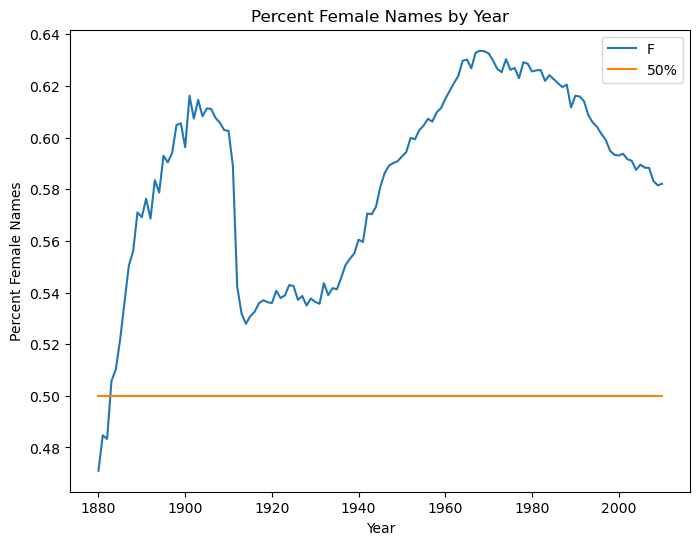
To augment the Solution 2 plot with a 50% line , we can use a DataFrame
wrapper containing f_row (as a column) and add a new column for the
50% line.
df2 = pd.DataFrame(f_row)
df2['50%'] = .5
df2.plot(ylabel='Percent Female Names',xlabel='Year',
title='Percent Female Names by Year', figsize=(8,6))
<AxesSubplot:title={'center':'Percent Female Names by Year'}, xlabel='Year', ylabel='Percent Female Names'>
The lesson of solution 2: If what you’re doing is a pretty standard
piece of data analysis, chances are good that pandas includes a
simple way of doing it.
Read some documentation to find potential tools. Consult stackoverflow for code snippets and pointers on where to look in the doumentation.
7.1.16. Complaints: a new dataset¶
We’re going to use a new dataset here, to demonstrate how to deal with datasets with few numerical attributes.
The next cell provides a URL for a subset of the of 311 service requests from NYC Open Data.
import os.path
#How to break up long strings into multiline segments
#Note the use of "line continued" character \
data_url = 'https://raw.githubusercontent.com/gawron/python-for-social-science/master/'\
'pandas/datasets/311-service-requests.csv'
import pandas as pd
# Some columns are of mixed types. This is OK. But we have to set
# low_memory=False
complaints = pd.read_csv(data_url,low_memory=False)
complaints.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 111069 entries, 0 to 111068
Data columns (total 52 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Unique Key 111069 non-null int64
1 Created Date 111069 non-null object
2 Closed Date 60270 non-null object
3 Agency 111069 non-null object
4 Agency Name 111069 non-null object
5 Complaint Type 111069 non-null object
6 Descriptor 110613 non-null object
7 Location Type 79022 non-null object
8 Incident Zip 98807 non-null object
9 Incident Address 84441 non-null object
10 Street Name 84432 non-null object
11 Cross Street 1 84728 non-null object
12 Cross Street 2 84005 non-null object
13 Intersection Street 1 19364 non-null object
14 Intersection Street 2 19366 non-null object
15 Address Type 102247 non-null object
16 City 98854 non-null object
17 Landmark 95 non-null object
18 Facility Type 19104 non-null object
19 Status 111069 non-null object
20 Due Date 39239 non-null object
21 Resolution Action Updated Date 96507 non-null object
22 Community Board 111069 non-null object
23 Borough 111069 non-null object
24 X Coordinate (State Plane) 98143 non-null float64
25 Y Coordinate (State Plane) 98143 non-null float64
26 Park Facility Name 111069 non-null object
27 Park Borough 111069 non-null object
28 School Name 111069 non-null object
29 School Number 111048 non-null object
30 School Region 110524 non-null object
31 School Code 110524 non-null object
32 School Phone Number 111069 non-null object
33 School Address 111069 non-null object
34 School City 111069 non-null object
35 School State 111069 non-null object
36 School Zip 111069 non-null object
37 School Not Found 38984 non-null object
38 School or Citywide Complaint 0 non-null float64
39 Vehicle Type 99 non-null object
40 Taxi Company Borough 117 non-null object
41 Taxi Pick Up Location 1059 non-null object
42 Bridge Highway Name 185 non-null object
43 Bridge Highway Direction 185 non-null object
44 Road Ramp 180 non-null object
45 Bridge Highway Segment 219 non-null object
46 Garage Lot Name 49 non-null object
47 Ferry Direction 24 non-null object
48 Ferry Terminal Name 70 non-null object
49 Latitude 98143 non-null float64
50 Longitude 98143 non-null float64
51 Location 98143 non-null object
dtypes: float64(5), int64(1), object(46)
memory usage: 44.1+ MB
Note that the df.info() summary shows how many non-null values there
are in each column, so that you can see there are some columns with very
few meaningful entries.
You can see null-entries in the first 5 rows: They are the entries
printed out as NaN.
NaN is short for “Not a Number”. It is the standard representation
of an undefined result for a numerical calculation. Here it is being
used to mean “No data entered here”; NaN is very commonly used with
this meaning in pandas, even in columns that do not have a numerical
type; we could, alternatively, use Python None for this purpose.
complaints[:5]
| Unique Key | Created Date | Closed Date | Agency | Agency Name | Complaint Type | Descriptor | Location Type | Incident Zip | Incident Address | ... | Bridge Highway Name | Bridge Highway Direction | Road Ramp | Bridge Highway Segment | Garage Lot Name | Ferry Direction | Ferry Terminal Name | Latitude | Longitude | Location | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 26589651 | 10/31/2013 02:08:41 AM | NaN | NYPD | New York City Police Department | Noise - Street/Sidewalk | Loud Talking | Street/Sidewalk | 11432 | 90-03 169 STREET | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 40.708275 | -73.791604 | (40.70827532593202, -73.79160395779721) |
| 1 | 26593698 | 10/31/2013 02:01:04 AM | NaN | NYPD | New York City Police Department | Illegal Parking | Commercial Overnight Parking | Street/Sidewalk | 11378 | 58 AVENUE | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 40.721041 | -73.909453 | (40.721040535628305, -73.90945306791765) |
| 2 | 26594139 | 10/31/2013 02:00:24 AM | 10/31/2013 02:40:32 AM | NYPD | New York City Police Department | Noise - Commercial | Loud Music/Party | Club/Bar/Restaurant | 10032 | 4060 BROADWAY | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 40.843330 | -73.939144 | (40.84332975466513, -73.93914371913482) |
| 3 | 26595721 | 10/31/2013 01:56:23 AM | 10/31/2013 02:21:48 AM | NYPD | New York City Police Department | Noise - Vehicle | Car/Truck Horn | Street/Sidewalk | 10023 | WEST 72 STREET | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 40.778009 | -73.980213 | (40.7780087446372, -73.98021349023975) |
| 4 | 26590930 | 10/31/2013 01:53:44 AM | NaN | DOHMH | Department of Health and Mental Hygiene | Rodent | Condition Attracting Rodents | Vacant Lot | 10027 | WEST 124 STREET | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 40.807691 | -73.947387 | (40.80769092704951, -73.94738703491433) |
5 rows × 52 columns
Selecting columns and rows in Complaints
As before we can select a column, by indexing with the name of the column:
complaints['Complaint Type']
0 Noise - Street/Sidewalk
1 Illegal Parking
2 Noise - Commercial
3 Noise - Vehicle
4 Rodent
...
111064 Maintenance or Facility
111065 Illegal Parking
111066 Noise - Street/Sidewalk
111067 Noise - Commercial
111068 Blocked Driveway
Name: Complaint Type, Length: 111069, dtype: object
As above we select rows by constructing Boolean Series:
nypd_bool = (complaints['Agency'] == 'NYPD')
nypd_bool[:10]
0 True
1 True
2 True
3 True
4 False
5 True
6 True
7 True
8 True
9 True
Name: Agency, dtype: bool
We construct a sub frame that has only Police Department complaints.
nypd_df = complaints[nypd_bool]
But there are 20 kinds of PD complaints in this data.
complaint_set = nypd_df['Complaint Type'].unique()
complaint_set
array(['Noise - Street/Sidewalk', 'Illegal Parking', 'Noise - Commercial',
'Noise - Vehicle', 'Blocked Driveway', 'Noise - House of Worship',
'Homeless Encampment', 'Noise - Park', 'Drinking', 'Panhandling',
'Derelict Vehicle', 'Bike/Roller/Skate Chronic', 'Animal Abuse',
'Traffic', 'Vending', 'Graffiti', 'Posting Advertisement',
'Urinating in Public', 'Disorderly Youth', 'Illegal Fireworks'],
dtype=object)
So we limit it further:
il_df = nypd_df[nypd_df['Complaint Type'] == 'Illegal Parking']
More constraints means progressively smaller DataFrames:
(len(complaints), len(nypd_df), len(il_df))
(111069, 15295, 3343)
Attribute syntax versus indexing syntax
Note that columns can also be specified using instance/attribute syntax, as in:
complaints.Agency
0 NYPD
1 NYPD
2 NYPD
3 NYPD
4 DOHMH
...
111064 DPR
111065 NYPD
111066 NYPD
111067 NYPD
111068 NYPD
Name: Agency, Length: 111069, dtype: object
But also note that doesnt work for the column name Complaint Type;
because this has a space, trying to use it as an attribute raises a
SyntaxError: No Python name can contain a space; that includes
attribute names.
complaints.Complaint Type
File "/var/folders/_q/2s1hy5bx1l7f9j1lw9zjgt19_wb463/T/ipykernel_64611/2805497044.py", line 1
complaints.Complaint Type
^
SyntaxError: invalid syntax
So the general Python syntax for indexing a container (square bracket syntax)
complaints['Complaint Type']
is the one to remember.
The indexing syntax is also the one that extends to accommodate
selection of multiple columns, using the fancy-indexing convention from
numpy (index via an arbitrary sequence of indices).
complaints[['Complaint Type', 'Borough']][:10]
| Complaint Type | Borough | |
|---|---|---|
| 0 | Noise - Street/Sidewalk | QUEENS |
| 1 | Illegal Parking | QUEENS |
| 2 | Noise - Commercial | MANHATTAN |
| 3 | Noise - Vehicle | MANHATTAN |
| 4 | Rodent | MANHATTAN |
| 5 | Noise - Commercial | QUEENS |
| 6 | Blocked Driveway | QUEENS |
| 7 | Noise - Commercial | QUEENS |
| 8 | Noise - Commercial | MANHATTAN |
| 9 | Noise - Commercial | BROOKLYN |
Narrowing down the set of columns is a common step, especially important when performing further analytical caulculations like pivot tables.
7.1.16.1. Using crosstab with the complaints data¶
The idea of crosstabulation has already arisen. In its simplest form, cross-tabulation is just getting the coocurrence counts of two attributes. In the complaints domain, for example, we might be interested in how often each complaint tyope occurs in each borough.
Crosstab Problem A: For each complaint type, find its frequency in each borough.
This is a cross-tabulation question: We use crosstab to get the
joint distribution counts for two attributes.
pd.crosstab(complaints['Agency'],complaints['Borough'])
| Borough | BRONX | BROOKLYN | MANHATTAN | QUEENS | STATEN ISLAND | Unspecified |
|---|---|---|---|---|---|---|
| Agency | ||||||
| 3-1-1 | 0 | 8 | 11 | 12 | 1 | 60 |
| CHALL | 0 | 0 | 0 | 0 | 0 | 77 |
| COIB | 0 | 0 | 0 | 0 | 0 | 1 |
| DCA | 155 | 357 | 358 | 284 | 36 | 215 |
| DEP | 791 | 2069 | 3419 | 1916 | 690 | 12 |
| DFTA | 4 | 5 | 3 | 3 | 0 | 7 |
| DHS | 6 | 31 | 54 | 8 | 0 | 2 |
| DOB | 358 | 775 | 477 | 1257 | 147 | 0 |
| DOE | 17 | 26 | 24 | 15 | 7 | 8 |
| DOF | 78 | 149 | 215 | 116 | 6 | 5806 |
| DOHMH | 657 | 891 | 913 | 602 | 174 | 0 |
| DOITT | 3 | 8 | 15 | 2 | 3 | 0 |
| DOP | 0 | 0 | 0 | 0 | 0 | 2 |
| DOT | 2605 | 5313 | 4182 | 4164 | 1123 | 320 |
| DPR | 438 | 1292 | 407 | 1934 | 532 | 11 |
| DSNY | 1094 | 2966 | 1167 | 2579 | 563 | 16 |
| EDC | 1 | 23 | 66 | 9 | 0 | 0 |
| FDNY | 6 | 17 | 517 | 52 | 10 | 29 |
| HPD | 11493 | 13871 | 7866 | 4986 | 851 | 0 |
| HRA | 0 | 0 | 0 | 0 | 0 | 392 |
| NYPD | 1933 | 4886 | 3657 | 4154 | 663 | 2 |
| OATH | 0 | 0 | 0 | 0 | 0 | 4 |
| OEM | 0 | 0 | 0 | 0 | 0 | 29 |
| OMB | 0 | 0 | 0 | 0 | 0 | 1 |
| OPS | 0 | 0 | 0 | 0 | 0 | 8 |
| TLC | 47 | 203 | 937 | 188 | 11 | 105 |
Elaboration of Crosstab Problem A: For each complaint type, find its frequency in each borough. Also give the total number of complaints by borough and by complaint type.
ct_agency_borough = pd.crosstab(complaints['Agency'],complaints['Borough'],margins=True)
ct_agency_borough
| Borough | BRONX | BROOKLYN | MANHATTAN | QUEENS | STATEN ISLAND | Unspecified | All |
|---|---|---|---|---|---|---|---|
| Agency | |||||||
| 3-1-1 | 0 | 8 | 11 | 12 | 1 | 60 | 92 |
| CHALL | 0 | 0 | 0 | 0 | 0 | 77 | 77 |
| COIB | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| DCA | 155 | 357 | 358 | 284 | 36 | 215 | 1405 |
| DEP | 791 | 2069 | 3419 | 1916 | 690 | 12 | 8897 |
| DFTA | 4 | 5 | 3 | 3 | 0 | 7 | 22 |
| DHS | 6 | 31 | 54 | 8 | 0 | 2 | 101 |
| DOB | 358 | 775 | 477 | 1257 | 147 | 0 | 3014 |
| DOE | 17 | 26 | 24 | 15 | 7 | 8 | 97 |
| DOF | 78 | 149 | 215 | 116 | 6 | 5806 | 6370 |
| DOHMH | 657 | 891 | 913 | 602 | 174 | 0 | 3237 |
| DOITT | 3 | 8 | 15 | 2 | 3 | 0 | 31 |
| DOP | 0 | 0 | 0 | 0 | 0 | 2 | 2 |
| DOT | 2605 | 5313 | 4182 | 4164 | 1123 | 320 | 17707 |
| DPR | 438 | 1292 | 407 | 1934 | 532 | 11 | 4614 |
| DSNY | 1094 | 2966 | 1167 | 2579 | 563 | 16 | 8385 |
| EDC | 1 | 23 | 66 | 9 | 0 | 0 | 99 |
| FDNY | 6 | 17 | 517 | 52 | 10 | 29 | 631 |
| HPD | 11493 | 13871 | 7866 | 4986 | 851 | 0 | 39067 |
| HRA | 0 | 0 | 0 | 0 | 0 | 392 | 392 |
| NYPD | 1933 | 4886 | 3657 | 4154 | 663 | 2 | 15295 |
| OATH | 0 | 0 | 0 | 0 | 0 | 4 | 4 |
| OEM | 0 | 0 | 0 | 0 | 0 | 29 | 29 |
| OMB | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| OPS | 0 | 0 | 0 | 0 | 0 | 8 | 8 |
| TLC | 47 | 203 | 937 | 188 | 11 | 105 | 1491 |
| All | 19686 | 32890 | 24288 | 22281 | 4817 | 7107 | 111069 |
Now ct_agency_borough contains both an 'All' column (containing
the sum of the values in each row) and an 'All' row (containing the
sum of the values for each column).
Note that as long as there are no rows missing an 'Agency' or
'Borough' (there aren’t), then ct_agency_borough['All']['All']
is the total number of rows in complaints.
print(len(complaints))
print(ct_agency_borough['All']['All'])
111069
111069
Complaints Problem B: What’s the noisiest borough? A little preprocessing is required. Then we can turn this into a cross tabulation of a restricted set of complaint types and borough.
# Apply a function that returns True if a string starts with 'noise'
# to every element of the Complaint Type column, producing a Boolean Series
# Roughly equivalent to
# boolean_series = pd.Series([ct.startswith('Noise')
# for ct in complaints['Complaint Type']])
boolean_series = complaints['Complaint Type'].apply(lambda x: x.startswith('Noise'))
complaints_noise = complaints[boolean_series]
complaints_noise[:5]
| Unique Key | Created Date | Closed Date | Agency | Agency Name | Complaint Type | Descriptor | Location Type | Incident Zip | ... | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 26589651 | 10/31/2013 02:08:41 AM | NaN | NYPD | New York City Police Department | Noise - Street/Sidewalk | Loud Talking | Street/Sidewalk | 11432 | ... |
| 2 | 26594139 | 10/31/2013 02:00:24 AM | 10/31/2013 02:40:32 AM | NYPD | New York City Police Department | Noise - Commercial | Loud Music/Party | Club/Bar/Restaurant | 10032 | ... |
| 5 | 26592370 | 10/31/2013 01:46:52 AM | NaN | NYPD | New York City Police Department | Noise - Commercial | Banging/Pounding | Club/Bar/Restaurant | 11372 | ... |
So what’s the noisiest borough? The answer is no surprise to those who’ve been in NYC.
ct_noise = pd.crosstab(complaints_noise['Borough'],complaints_noise['Complaint Type'],
margins=True)
ct_noise.sort_values(by = 'All',ascending=False)
| Complaint Type | Noise | Noise - Commercial | Noise - Helicopter | Noise - House of Worship | Noise - Park | Noise - Street/Sidewalk | Noise - Vehicle | All |
|---|---|---|---|---|---|---|---|---|
| Borough | ||||||||
| All | 3321 | 2578 | 99 | 67 | 191 | 1928 | 750 | 8934 |
| MANHATTAN | 1848 | 1140 | 66 | 16 | 91 | 917 | 255 | 4333 |
| BROOKLYN | 767 | 775 | 23 | 23 | 60 | 456 | 237 | 2341 |
| QUEENS | 418 | 451 | 9 | 15 | 27 | 226 | 130 | 1276 |
| BRONX | 168 | 136 | 1 | 11 | 9 | 292 | 102 | 719 |
| STATEN ISLAND | 115 | 76 | 0 | 2 | 4 | 36 | 25 | 258 |
| Unspecified | 5 | 0 | 0 | 0 | 0 | 1 | 1 | 7 |
Complaints problem C
Find the complaint counts for three agences (‘DOT’, “DOP”, ‘NYPD’).
First Produce a DataFrame containing only the three agencies DT, DOP and NYPD. This part is easy.
pt00 = complaints[complaints.Agency.isin(['DOT', "DOP", 'NYPD'])]
The frame pt00 now restricts us to three agencies.
Second, use pt00 to create a DataFrame or Series whose index is the
complaint types and whose three columns are the Three Agencies. Each
cell should contain the count of the complaint type of that row and the
agency of that column. For example, the number in the 'Animal Abuse'
row in the 'NYPD' column should be the number of NYPD complaints
about animal abuse (which happens to be 164).
three = ['DOT', "DOP", 'NYPD']
pt00 = complaints[complaints.Agency.isin(three)]
pd.crosstab(pt00['Complaint Type'], pt00['Agency'])
| Agency | DOP | DOT | NYPD |
|---|---|---|---|
| Complaint Type | |||
| Agency Issues | 0 | 20 | 0 |
| Animal Abuse | 0 | 0 | 164 |
| Bike Rack Condition | 0 | 7 | 0 |
| Bike/Roller/Skate Chronic | 0 | 0 | 32 |
| Blocked Driveway | 0 | 0 | 4590 |
| Bridge Condition | 0 | 20 | 0 |
| Broken Muni Meter | 0 | 2070 | 0 |
| Bus Stop Shelter Placement | 0 | 14 | 0 |
| Compliment | 0 | 1 | 0 |
| Curb Condition | 0 | 66 | 0 |
| DOT Literature Request | 0 | 123 | 0 |
| Derelict Vehicle | 0 | 0 | 803 |
| Disorderly Youth | 0 | 0 | 26 |
| Drinking | 0 | 0 | 83 |
| Ferry Complaint | 0 | 4 | 0 |
| Ferry Inquiry | 0 | 32 | 0 |
| Ferry Permit | 0 | 1 | 0 |
| Graffiti | 0 | 0 | 13 |
| Highway Condition | 0 | 130 | 0 |
| Highway Sign - Damaged | 0 | 1 | 0 |
| Homeless Encampment | 0 | 0 | 269 |
| Illegal Fireworks | 0 | 0 | 3 |
| Illegal Parking | 0 | 0 | 3343 |
| Invitation | 1 | 0 | 0 |
| Municipal Parking Facility | 0 | 1 | 0 |
| Noise - Commercial | 0 | 0 | 2578 |
| Noise - House of Worship | 0 | 0 | 67 |
| Noise - Park | 0 | 0 | 191 |
| Noise - Street/Sidewalk | 0 | 0 | 1928 |
| Noise - Vehicle | 0 | 0 | 750 |
| Panhandling | 0 | 0 | 23 |
| Parking Card | 0 | 8 | 0 |
| Posting Advertisement | 0 | 0 | 5 |
| Public Toilet | 0 | 6 | 0 |
| Request for Information | 1 | 0 | 0 |
| Sidewalk Condition | 0 | 339 | 0 |
| Street Condition | 0 | 3473 | 0 |
| Street Light Condition | 0 | 7117 | 0 |
| Street Sign - Damaged | 0 | 691 | 0 |
| Street Sign - Dangling | 0 | 110 | 0 |
| Street Sign - Missing | 0 | 327 | 0 |
| Traffic | 0 | 0 | 168 |
| Traffic Signal Condition | 0 | 3145 | 0 |
| Tunnel Condition | 0 | 1 | 0 |
| Urinating in Public | 0 | 0 | 30 |
| Vending | 0 | 0 | 229 |
**Crosstab Problem D: What’s the most common complaint type?
Note: This is not a question requiring cross-tabulation.
Cross tabulation is for looking at co-occurrence counts of more than
one column. This is about sorting the counts
of the values occurring in one column, "Complaint Type"
For this we use the series method .value_counts()
which by default sorts the counts.
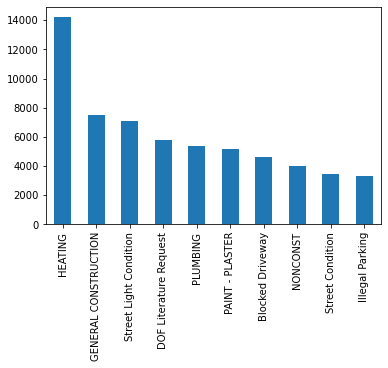
complaint_counts = complaints['Complaint Type'].value_counts()
complaint_counts
HEATING 14200
GENERAL CONSTRUCTION 7471
Street Light Condition 7117
DOF Literature Request 5797
PLUMBING 5373
...
Municipal Parking Facility 1
Tunnel Condition 1
DHS Income Savings Requirement 1
Stalled Sites 1
X-Ray Machine/Equipment 1
Name: Complaint Type, Length: 165, dtype: int64
Since complaints_counts is a Series (the complaint types are the
index) ordered by number of complaints, we can plot the numbers for the
top complaint types, demonstrating visually what an outlier Heating
is (Oh those NYC winters!).
complaint_counts[:10].plot(kind='bar')
<AxesSubplot:>
Crosstab understanding exercise
Find the distribution of complaint Statuses. That is, write an expression that produces a DataFrame or Series whose index is the seven possible complaint Statuses and whose values are the number of complaints with each Status.
To help you check your solution, here are the seven complaint statuses.
set(complaints['Status'])
{'Assigned',
'Closed',
'Email Sent',
'Open',
'Pending',
'Started',
'Unassigned'}
sc = complaints['Status'].value_counts()
sc
Closed 57165
Open 43972
Assigned 6189
Pending 3165
Started 447
Email Sent 129
Unassigned 2
Name: Status, dtype: int64
7.1.17. Using groupby¶
Grouping is a fundamental data analysis operation. For example, it is the first step in doing a cross-tabulation. We will also see that it us the first step in creating a pivot table.
As these examples suggest, we’re mostly interested in grouping as a
preliminary step in performing statistical analysis, but it is useful to
look at in isolation first, using the basic groupby function that
pandas provides.
Let’s use a new dataset to illustrate, because it has some very natural groupings.
nba_file_url = 'https://gawron.sdsu.edu/python_for_ss/course_core/data/nba.csv'
nba_df = pd.read_csv(nba_file_url)
Each row contains information about one current player. The team rosters are listed in alphabetical order of team name, with the players in alphabetical order by name within the teams.
nba_df[:5]
| Name | Team | Number | Position | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Avery Bradley | Boston Celtics | 0.0 | PG | 25.0 | 6-2 | 180.0 | Texas | 7730337.0 |
| 1 | Jae Crowder | Boston Celtics | 99.0 | SF | 25.0 | 6-6 | 235.0 | Marquette | 6796117.0 |
| 2 | John Holland | Boston Celtics | 30.0 | SG | 27.0 | 6-5 | 205.0 | Boston University | NaN |
| 3 | R.J. Hunter | Boston Celtics | 28.0 | SG | 22.0 | 6-5 | 185.0 | Georgia State | 1148640.0 |
| 4 | Jonas Jerebko | Boston Celtics | 8.0 | PF | 29.0 | 6-10 | 231.0 | NaN | 5000000.0 |
We are going to use it to find out about team salaries, height by position and weight by position.
We group the rows by team and then show the alphabetically first player in each team.
gt = nba_df.groupby('Team')
# First member of each team grouop for first 5 teams
gt.first()[:5]
| Name | Number | Position | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|---|
| Team | ||||||||
| Atlanta Hawks | Kent Bazemore | 24.0 | SF | 26.0 | 6-5 | 201.0 | Old Dominion | 2000000.0 |
| Boston Celtics | Avery Bradley | 0.0 | PG | 25.0 | 6-2 | 180.0 | Texas | 7730337.0 |
| Brooklyn Nets | Bojan Bogdanovic | 44.0 | SG | 27.0 | 6-8 | 216.0 | Oklahoma State | 3425510.0 |
| Charlotte Hornets | Nicolas Batum | 5.0 | SG | 27.0 | 6-8 | 200.0 | Virginia Commonwealth | 13125306.0 |
| Chicago Bulls | Cameron Bairstow | 41.0 | PF | 25.0 | 6-9 | 250.0 | New Mexico | 845059.0 |
type(gt)
pandas.core.groupby.generic.DataFrameGroupBy
Here we’ve created a DataFrameGroupBy instance that split the player
data into subgroups, the players belonging to each team.
We can display one of those groups as follows:
# A particular group
gt.get_group('Utah Jazz')[:5]
| Name | Team | Number | Position | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|---|---|
| 442 | Trevor Booker | Utah Jazz | 33.0 | PF | 28.0 | 6-8 | 228.0 | Clemson | 4775000.0 |
| 443 | Trey Burke | Utah Jazz | 3.0 | PG | 23.0 | 6-1 | 191.0 | Michigan | 2658240.0 |
| 444 | Alec Burks | Utah Jazz | 10.0 | SG | 24.0 | 6-6 | 214.0 | Colorado | 9463484.0 |
| 445 | Dante Exum | Utah Jazz | 11.0 | PG | 20.0 | 6-6 | 190.0 | NaN | 3777720.0 |
| 446 | Derrick Favors | Utah Jazz | 15.0 | PF | 24.0 | 6-10 | 265.0 | Georgia Tech | 12000000.0 |
This, however, is an odd use of a grouping object. If all we were
interested in was constructing a DataFrame limited to one team, we could
accomplished that much more easily with:
nba_df[nba_df['Team'] == 'Utah Jazz'][:5]
| Name | Team | Number | Position | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|---|---|
| 442 | Trevor Booker | Utah Jazz | 33.0 | PF | 28.0 | 6-8 | 228.0 | Clemson | 4775000.0 |
| 443 | Trey Burke | Utah Jazz | 3.0 | PG | 23.0 | 6-1 | 191.0 | Michigan | 2658240.0 |
| 444 | Alec Burks | Utah Jazz | 10.0 | SG | 24.0 | 6-6 | 214.0 | Colorado | 9463484.0 |
| 445 | Dante Exum | Utah Jazz | 11.0 | PG | 20.0 | 6-6 | 190.0 | NaN | 3777720.0 |
| 446 | Derrick Favors | Utah Jazz | 15.0 | PF | 24.0 | 6-10 | 265.0 | Georgia Tech | 12000000.0 |
The benefit of the grouping object is that it makes various comparisons based on the same grouping easier. Suppose, for example, that we were interested in comparing average team ages and average team salary. To make this more interested, let’s say we’re interested in looking at the degree of correlation team age and team salary.
Then we use our team grouping instance gt to look at both variables:
mean_age_by_team = gt['Age'].mean()
mean_salary_by_team = gt['Salary'].mean()
comp = pd.DataFrame(dict(Age=mean_age_by_team,
Salary=mean_salary_by_team))
comp[:5]
| Age | Salary | |
|---|---|---|
| Team | ||
| Atlanta Hawks | 28.200000 | 4.860197e+06 |
| Boston Celtics | 24.733333 | 4.181505e+06 |
| Brooklyn Nets | 25.600000 | 3.501898e+06 |
| Charlotte Hornets | 26.133333 | 5.222728e+06 |
| Chicago Bulls | 27.400000 | 5.785559e+06 |
And now it’s quite easy to summon up the correlation of Age and Salary viewed team by team.
#Uses pearsonr correlation
comp_corr = comp.corr()
#Add some color coding to highlight the strong correlations.
comp_corr.style.background_gradient(cmap='coolwarm')
| Age | Salary | |
|---|---|---|
| Age | 1.000000 | 0.716125 |
| Salary | 0.716125 | 1.000000 |
The DataFrame.corr() method always produces a square NxN
DataFrame. When there are more than two columns, all pairwise
correlations are computed. When seeking pairwise correlation only
between two columns, use Series.corr:
comp['Age'].corr(comp['Salary'], method='kendall')
0.6398163039514194
Notice that in order to run the .corr() method on the
DataFrame comp we first had to create comp with the right index
and columns. We did that in line 3 in the cell computing the group
means:
comp = pd.DataFrame(dict(Age=mean_age_by_team,
Salary=mean_salary_by_team))
Creating this DataFrame was step three of a three-step process:
Grouping by team (sometimes called splitting)
gt = nba_df.groupby('Team')
Applying a statistical aggregation function (
.mean(...))mean_age_by_team = gt['Age'].mean()mean_salary_by_team = gt['Salary'].mean()
Combining the results into a
DataFramepd.DataFrame(dict(Age=mean_age_by_team, Salary=mean_salary_by_team))
These three steps collectively are called the Split/Apply/Combine
strategy. They arise often enough in Statistical Data Analysis to
deserve packaging into a single function called pivot_table. For
example, to get the mean ages and salaries team by team, we do:
# Group the players into teams, take the mean age and salary for each time,
# make a datafra,
pd.pivot_table(nba_df,index='Team', values=["Salary","Age"],aggfunc='mean')[:5]
| Age | Salary | |
|---|---|---|
| Team | ||
| Atlanta Hawks | 28.200000 | 4.860197e+06 |
| Boston Celtics | 24.733333 | 4.181505e+06 |
| Brooklyn Nets | 25.600000 | 3.501898e+06 |
| Charlotte Hornets | 26.133333 | 5.222728e+06 |
| Chicago Bulls | 27.400000 | 5.785559e+06 |
Ths is exactly the same DataFrame we saw before created in one step.
We’ll have quite a bit more to say about pivot tables in the second
pandas notebook. For now let’s continue exploring the uses of
grouping.
There are two motivations for pandas to provide users with direct
acces to groupby instances.
A single
groupbyinstance can support the analysis of multiple variables, possibly with different aggregation functions (in our salart and age example we used mean twice).Grouping can also be done using more than one variable.
Let’s illustrate point (2) by grouping by team and position.
In basketball each team puts five players on the court at any given time. Although the specialized roles of the players on the court are changing, classically a player plays one of five positions:
Point Guard (PG)
Shooting Guard (SG)
Small Forward (SF)
Power Forward (PF)
Center (C).
This data set assigns each player to one of these five positions. A team will typically have multiple players assigned to any given position.
gtp = nba_df.groupby(['Team','Position'])
# Show the first entry for each team/position pair
gtp.first()
| Name | Number | Age | Height | Weight | College | Salary | ||
|---|---|---|---|---|---|---|---|---|
| Team | Position | |||||||
| Atlanta Hawks | C | Al Horford | 15.0 | 30.0 | 6-10 | 245.0 | Florida | 12000000.0 |
| PF | Kris Humphries | 43.0 | 31.0 | 6-9 | 235.0 | Minnesota | 1000000.0 | |
| PG | Dennis Schroder | 17.0 | 22.0 | 6-1 | 172.0 | Wake Forest | 1763400.0 | |
| SF | Kent Bazemore | 24.0 | 26.0 | 6-5 | 201.0 | Old Dominion | 2000000.0 | |
| SG | Tim Hardaway Jr. | 10.0 | 24.0 | 6-6 | 205.0 | Michigan | 1304520.0 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Washington Wizards | C | Marcin Gortat | 13.0 | 32.0 | 6-11 | 240.0 | North Carolina State | 11217391.0 |
| PF | Drew Gooden | 90.0 | 34.0 | 6-10 | 250.0 | Kansas | 3300000.0 | |
| PG | Ramon Sessions | 7.0 | 30.0 | 6-3 | 190.0 | Nevada | 2170465.0 | |
| SF | Jared Dudley | 1.0 | 30.0 | 6-7 | 225.0 | Boston College | 4375000.0 | |
| SG | Alan Anderson | 6.0 | 33.0 | 6-6 | 220.0 | Michigan State | 4000000.0 |
149 rows × 7 columns
gtp_first is a DataFrame with a double index (an index with two
levels) so we can select an index member from the first level to get a
set of rows.
The alphabetically first players on the Boston Celtics, by position.
#
gtp.first().loc['Boston Celtics']
| Name | Number | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|
| Position | |||||||
| C | Kelly Olynyk | 41.0 | 25.0 | 7-0 | 238.0 | Gonzaga | 2165160.0 |
| PF | Jonas Jerebko | 8.0 | 29.0 | 6-10 | 231.0 | LSU | 5000000.0 |
| PG | Avery Bradley | 0.0 | 25.0 | 6-2 | 180.0 | Texas | 7730337.0 |
| SF | Jae Crowder | 99.0 | 25.0 | 6-6 | 235.0 | Marquette | 6796117.0 |
| SG | John Holland | 30.0 | 27.0 | 6-5 | 205.0 | Boston University | 1148640.0 |
gtp.first().loc['Golden State Warriors']
| Name | Number | Age | Height | Weight | College | Salary | |
|---|---|---|---|---|---|---|---|
| Position | |||||||
| C | Andrew Bogut | 12.0 | 31.0 | 7-0 | 260.0 | Utah | 13800000.0 |
| PF | Draymond Green | 23.0 | 26.0 | 6-7 | 230.0 | Michigan State | 14260870.0 |
| PG | Stephen Curry | 30.0 | 28.0 | 6-3 | 190.0 | Davidson | 11370786.0 |
| SF | Harrison Barnes | 40.0 | 24.0 | 6-8 | 225.0 | North Carolina | 3873398.0 |
| SG | Leandro Barbosa | 19.0 | 33.0 | 6-3 | 194.0 | Belmont | 2500000.0 |
To get to an individual player record (a row) you need to supply an index member from each level.
So the alphabetically first center on the Boston Celtics is:
gtp.first().loc[('Boston Celtics','C')]
Name Kelly Olynyk
Number 41.0
Age 25.0
Height 7-0
Weight 238.0
College Gonzaga
Salary 2165160.0
Name: (Boston Celtics, C), dtype: object
Now a DataFrameGroupBy instance is not a DataFrame or a Series,
making groupby one of the few commonly used pandas analysis
methods that doesn’t return either:
gtp
<pandas.core.groupby.generic.DataFrameGroupBy object at 0x7fd6c3fdfa20>
But one can do many of the things one does to a DataFrame to a
GroupByDataFrame instance. For example, extract a column:
gtp['Salary']
<pandas.core.groupby.generic.SeriesGroupBy object at 0x7fd69ca46438>
Which yields a SeriesGroupBy instance. Which has many of the same
methods we saw for the DataFrameGroupBy instances above, including
.first() and .get_group().
Instead of calling either of those, let’s apply an aggregation function appropriate to this column:
salary_df = gtp['Salary'].mean()
This gets us a new Series, doubly indexed by team and position:
type(salary_df)
pandas.core.series.Series
salary_df.iloc[:14]
Team Position
Atlanta Hawks C 7.585417e+06
PF 5.988067e+06
PG 4.881700e+06
SF 3.000000e+06
SG 2.607758e+06
Boston Celtics C 2.450465e+06
PF 6.056987e+06
PG 4.974652e+06
SF 6.796117e+06
SG 2.107997e+06
Brooklyn Nets C 1.031814e+07
PF 3.576205e+06
PG 2.915759e+06
SG 1.473351e+06
Name: Salary, dtype: float64
salary_df.loc['Boston Celtics']
Position
C 2.450465e+06
PF 6.056987e+06
PG 4.974652e+06
SF 6.796117e+06
SG 2.107997e+06
Name: Salary, dtype: float64
salary_df.loc['Boston Celtics']['C']
2450465.0
Sample Interpretation: The Celtics pays their centers an average of 2.4 Million.
Now we can do things like the following.
Compare Golden State salaries with Boston salaries position by position.
salary_df.loc['Boston Celtics']
Position
C 2.450465e+06
PF 6.056987e+06
PG 4.974652e+06
SF 6.796117e+06
SG 2.107997e+06
Name: Salary, dtype: float64
salary_df.loc['Golden State Warriors']
Position
C 6.541249e+06
PF 7.275312e+06
PG 8.457256e+06
SF 3.766367e+06
SG 6.316092e+06
Name: Salary, dtype: float64
salary_df.loc['Golden State Warriors'] > salary_df.loc['Boston Celtics']
Position
C True
PF True
PG True
SF False
SG True
Name: Salary, dtype: bool
The Warriors pay more at every position but small forward (SF).
Each of these is a Series so in theory we can take the mean again:
salary_df = gtp['Salary'].mean()
print(f'{salary_df.loc["Boston Celtics"].mean():6,.2f}')
print(f'{salary_df.loc["Golden State Warriors"].mean():6,.2f}')
#salary_df.loc['Golden State Warriors'].mean())
4,477,243.37
6,471,255.35
But these numbers may not have the interpretation you think they do.
In order to get the right interpretation of the above numbers, think about why the following numbers aren’t the same.
salary_df2 = gt['Salary'].mean()
print(f'{salary_df2.loc["Boston Celtics"]:6,.2f}')
print(f'{salary_df2.loc["Golden State Warriors"]:6,.2f}')
4,181,504.86
5,924,599.80
7.1.18. Understanding cross-tabulation¶
With the help of the grouping operation we’re now in a position to be able to characterize cross-tabulation a little more generally.
Grouping is the first step in cross-tabulation (which actually uses all three steps of the split/apply/combine strategy).
Let’s take our group-by-team-and-position object and compute the size of each group.
The result is a doubly indexed Series containing group sizes:
# This with-construction executes code in a CONTEXT
# which then goes away after the code block is exited.
# Here we ask pandas to print more than the default number of rows
with pd.option_context('display.max_rows', None):
print(type(gtp['Name'].count()))
print(gtp['Name'].count()[:19])
<class 'pandas.core.series.Series'>
Team Position
Atlanta Hawks C 3
PF 4
PG 2
SF 2
SG 4
Boston Celtics C 3
PF 3
PG 4
SF 1
SG 4
Brooklyn Nets C 2
PF 4
PG 3
SG 6
Charlotte Hornets C 3
PF 3
PG 3
SF 1
SG 5
Name: Name, dtype: int64
This is exactly the same information we would get with a cross-tabulation, except that the result is packaged in a singly indexed DataFrame with multiple columns:
tp_ct = pd.crosstab(nba_df['Team'], nba_df['Position'],margins=True)
print(type(tp_ct))
tp_ct[:4]
<class 'pandas.core.frame.DataFrame'>
| Position | C | PF | PG | SF | SG | All |
|---|---|---|---|---|---|---|
| Team | ||||||
| Atlanta Hawks | 3 | 4 | 2 | 2 | 4 | 15 |
| Boston Celtics | 3 | 3 | 4 | 1 | 4 | 15 |
| Brooklyn Nets | 2 | 4 | 3 | 0 | 6 | 15 |
| Charlotte Hornets | 3 | 3 | 3 | 1 | 5 | 15 |
| .... | ||||||
| All | 78 | 100 | 92 | 85 | 102 | 457 |
It is useful to think of cross-tabulation in terms of the split/apply/combine strategy.
Splitting the data into the groups defined by the input sequences.
Applying the operation of counting to the groups.
Combining the results into a DataFrame.
We will return to the split/apply/combine strategy in part two of the pandas introduction.
7.1.19. Exercises combining everything we’ve learned in Part One.¶
Try answering the following questions. Note. You may or may not have to
use groupby method in your answers. Even if you know how to use
pandas pivot_table function, try to avoid using that. Answers follow
a few cells down.
How many NBA players weigh under 220?
By position, how many players weigh under 220? How many do not? In other words, create a DataFrame whose index is position with two columns, False and True, which contain the counts of the players under and not under 220.
What is the average weight of Centers in the league? Which position is heavier on average, Center or Power Forward?
What is the average height of Centers in the league? Which position is taller on average, Center or Power Forward? Note: This is not just a boring minor variation on the previous question. There is a complication.
What position earns the highest salary on average?
What colleges have supplied the most current NBA players? How many colleges have supplied only one NBA player?
#1
#2
#3
#4
#5
#6
#7
Q1 How many NBA players weigh under 220?
len(nba_df[nba_df['Weight']<220])
205
Q2 By position, how many NBA players weigh under 220?
This is a cross tabulation question; for each position we want the distribution of counts of players over and under 220. The only problem is that we don’t have an over-under 220 column. So we use a Boolean constraint to create one (we don’t need to make it an official column). Then we do a cross-tabulation.
# a virtual new column
under_220 = nba_df['Weight']<220
wt_pos_ct = pd.crosstab(nba_df['Position'],under_220)
wt_pos_ct
| Weight | False | True |
|---|---|---|
| Position | ||
| C | 78 | 0 |
| PF | 98 | 2 |
| PG | 1 | 91 |
| SF | 54 | 31 |
| SG | 21 | 81 |
# Note the above answer is fine. But it's nice to supply a column name for our bogus column
# to clarify what's being shown
wt_pos_ct = pd.crosstab(nba_df['Position'],under_220,colnames=['Under 220'])
wt_pos_ct
| Under 220 | False | True |
|---|---|---|
| Position | ||
| C | 78 | 0 |
| PF | 98 | 2 |
| PG | 1 | 91 |
| SF | 54 | 31 |
| SG | 21 | 81 |
Q3 What is the average weight of Centers in the league?
gp = nba_df.groupby('Position')
weight_by_position = gp['Weight'].mean()
# This is a Series
weight_by_position
Position
C 254.205128
PF 240.430000
PG 189.478261
SF 221.776471
SG 206.686275
Name: Weight, dtype: float64
#Q1
print(weight_by_position['C'])
#Q2
print(weight_by_position['C'] > weight_by_position['SF'])
254.2051282051282
True
# Note also: This one is a natural pivot table question, with `weight_by_position` a DataFrame, not a Series
weight_by_position_df = pd.pivot_table(nba_df,index='Position',values='Weight',aggfunc='mean')
#print(weight_by_position_df['C'])
print(weight_by_position_df.loc['C'])
print()
print(weight_by_position_df.loc['C'] > weight_by_position_df.loc['SF'])
Weight 254.205128
Name: C, dtype: float64
Weight True
dtype: bool
Q4 What is the average height of Centers in the league?
It is a more challenging task to answer these same questions about heights.
This is because the entries in the height column are strings that need to be converted to numbers before a mean can be taken.
sample_height = nba_df['Height'].iloc[0]
sample_height
'6-2'
So we want to apply this function to every element of the Height Column.
def str_height_to_float_height(str_height):
if not isinstance(str_height,str):
# If, for example, it's already a float (especially a NaN), leave it
return str_height
(ft, inch) = [int(s) for s in str_height.split('-')]
return ft + inch/12
sample_height_float = str_height_to_float_height(sample_height)
sample_height_float
6.166666666666667
The pandas DataFrame and Series method apply applies a function
to each row of self and returns the results as an instance of the
same class as self with the same index.
In the next cell we apply str_height_to_float_height to the Series
nba_df['Height'] and get back another Series. We use it to make a
new column.
nba_df['HeightFloats'] = nba_df['Height'].apply(str_height_to_float_height)
nba_df['HeightFloats']
0 6.166667
1 6.500000
2 6.416667
3 6.416667
4 6.833333
...
453 6.250000
454 6.083333
455 7.250000
456 7.000000
457 NaN
Name: HeightFloats, Length: 458, dtype: float64
Now we do with this new column what we did with Weights.
height_by_position = gp['HeightFloats'].mean()
height_by_position
Position
C 6.941239
PF 6.809167
PG 6.202899
SF 6.632353
SG 6.461601
Name: HeightFloats, dtype: float64
#Height of centers
print(height_by_position['C'])
# Who's taller, centers or power forwards?
print(height_by_position['C'] > height_by_position['SF'])
6.941239316239316
True
The following might be a nice thing to do. Turn the mean heights back into normal-looking height strings.
def float_height_to_str(ft_height):
if isinstance(ft_height,float) and np.isnan(ft_height):
# If it's a NaN, leave it alone
return ft_height
# np.floor returns an int (mathematically) but its type is still float
(ft_int, inch_fl) = np.floor(ft_height), ft_height%1
return str(round(ft_int)) + '-' + str(round(inch_fl * 12))
height_by_position.apply(float_height_to_str)
Position
C 6-11
PF 6-10
PG 6-2
SF 6-8
SG 6-6
Name: HeightFloats, dtype: object
Q5 What position earns the highest salary on average?
gp = nba_df.groupby('Position')
gp['Salary'].mean().sort_values(ascending=False).index[0]
'C'
Q6 What colleges have supplied the most current NBA players?
Since there’s no cross tabulation of multiple columns here, and the
question involves counting values that are onfined to one column
('College'), this question does not require either grouping or a
pivot table.
The '.value_counts()' method does everything we need.
college_cts = nba_df['College'].value_counts()
college_cts[:5]
Kentucky 22
Duke 20
Kansas 18
North Carolina 16
UCLA 15
Name: College, dtype: int64
Q6 (ctd.) How many colleges have supplied only one NBA player?
We need to create a Series that contains the frequency of each count in
college_counts.
Then we can retrieve the frequency for 1 NBA player. That means using
the .value_counts() method on college_cts. Since the values in
the college_ counts Series are NBA player counts, applying
.value_counts() again will produce a Series whose index is NBA
player counts and whose values are the number of times each player count
has occurred; in this case that means the number of colleges that have
supplied that many NBA players.
For convenience, we’ll sort the index of the resulting Series.
college_cts.value_counts().sort_index()
1 52
2 24
3 15
4 5
5 4
6 6
7 3
8 1
9 1
10 1
13 1
15 1
16 1
18 1
20 1
22 1
Name: College, dtype: int64
So 52 colleges have supplied exactly one NBA player; 24 have supplied 2; 15 have supplied 3; and so one.
The expression for exactly the value we want is:
college_cts.value_counts().loc[1]
52
