6.1. Numpy arrays¶
import numpy as np
a = np.arange(15)
a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
The object named a in the cell above is called an array.
We used np.arange to define a; np.arange is like the builtin
Python function range, except that it produces an array in place of
a list. For now you can think of an array as sequence with only one
type. You can do various sequence-like things with arrays, such as
indexing by position and taking slices.
a[2]
2
a[2:5]
array([2, 3, 4])
There are some other differences between a and the ordinary Python
sequences we have learned about, but we can’t really talk about what
motivates arrays without looking at a different kind of example: The
characteristic feature of a sequence is that any item in it can
unambigously be accessed by a single integer; there’s a first postion
and the first position has a next position associated with it. In this
sense sequences are one-dimensional.
In addition to 1D sequences like a, numpy also provides 2D
arrays, which are tables of numbers. Here both row and column
structure matter.
An example:
#Make a 3x5 array from the range array we used above.
LL = np.arange(15).reshape((3,5))
print(LL)
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
LL is a 3x5 two-dimensional array. It has 3 rows and 5 columns.
To access any given value we need two integers, a 0-based row index paired with c 0-based column index.
LL[2,3]
13
Contrast that with the single index we need to retrieve the same value
from the original array a:
a[13]
13
So a has 1 dimension; LL has 2.
print(a)
print()
print(LL)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
Exercise
In the next cell an array P is created.
Write array-indexing expressions that retrieve the following values from
P.
13
8
26
Explain why P[2,8] raises an error while P[8,2] does not.
P = np.arange(27).reshape((9,3))
P
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17],
[18, 19, 20],
[21, 22, 23],
[24, 25, 26]])
P[2,2]
8
P[4,1]
13
P[2,2]
8
P[8,2]
26
The error message in the next cell refers to axis 1 which is the column
axis. Since the array is 9x3 and 0-based indexing is used for each
dimension, the maximum row index is 8 and the maximum column index is 2;
P[8,2] obeys these limits; the example in the next cell does not.
P[2,8]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Input In [303], in <cell line: 1>()
----> 1 P[2,8]
IndexError: index 8 is out of bounds for axis 1 with size 3
6.1.1. Different shapes for the same data¶
In the next cell four arrays are created, one 1D array a_1d of
length 15, and three 2D arrays, and each of the four arrays is printed.
We see some of the various ways of representing the same sequence of
numbers opened up by having two dimensions instead of just one.
To create the first two 2D arrays, the 1D array is reshaped; first
into a 3 by 5 array (array b; a 3 by 5 array has 3 rows and 2
columns), then into a 5 by 3 array (array c; a 5 by 3 array has 5
rows and 3 columns).
Finally, we create a third 2D array c by transposing b; note
that c has the same 3 by 5 shape as a, but is distinct from it.
a_1d = np.arange(15)
print('a_1d\n', a_1d)
a = np.arange(15).reshape(3, 5)
print('a\n', a)
b = np.arange(15).reshape(5, 3)
print('b\n',b)
c = b.transpose()
print('c\n',c)
a_1d
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
a
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
b
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]]
c
[[ 0 3 6 9 12]
[ 1 4 7 10 13]
[ 2 5 8 11 14]]
6.1.2. Arrays and Math¶
The need for 2D arrays is obvious if you’ve taken a linear algebra class. They correspond to the mathematical object called a matrix. One application for matrices is in solving systems of equations, and indeed numpy 2D arrays are routinely used to solve systems of equations, but this really only scratches the surface. A matrix can represent any linear map, and a linear map is a very general and very important mathematical idea. Examples of linear maps include rotation in 2D and 3D space, mappings from any coordinate system to any other coordinate system, and differentiation of polynomial functions.
A more immediate application for matrices for a data scientist is they can represent all that is known about a single data set. Generally each row represents an item (an individual or event in the data), and the entry in each column its value for a particular attribute. For example let’s say each room in a hotel has lamps, tables, chairs, and beds, but in varying numbers. We might represent the inventory of items in 5-room hotel with a 5x4 matrix (5 rows, 4 columns), as follows:
6 3 4 1
5 2 3 2
8 3 6 2
5 1 3 1
10 4 7 2
So the first row represents a room with 6 lamps, 3 tables, 4 chairs, and 1 bed. Now if we represent the cost of each item as 1D cost array (or vector) to use the mathematical term,
40 175 90 450,
where the costs are ordered in the same way as our columns above: lamps costs, table costs, chair costs, and bed costs. Then we can compute the first room furnishing costs as follows:
6*40 + 3*175 + 4*90 + 1*450
1575
Now the computation above can also be done as the “dot product” (or “dot”) of the first row of the room_matrix and the cost vector. The dot product of two 1D arrays is just the sum of the product of the corresponding terms in the two arrays (they need to be the same length). That is,
6*40 + 3*175 + 4*90 + 1*450
So one way of thinking of dot product — an operation of great importance in mathematics and physics (and many other contexts) — is just as a way of applying a particular sequence of coefficients — 6, 3, 4, and 1 here to a particular sequence of values — 40, 175, 90, and 450 here.
room_matrix = \
np.array(
[[6, 3, 4, 1],
[5, 2, 3, 2],
[8, 3, 6, 2],
[2, 1, 3, 5],
[10, 4, 7, 2]])
cost_vector = np.array([40, 175, 90, 450])
Computing the room cost for the first room:
room_matrix[0,:].dot(cost_vector)
1575
Mathematically, dot product is an operation that takes two vectors (sequences of values) and produces a scalar (a single number).
If we ask python for the dot product of an M x N array A with a 1D
N-array B, the result is a 1D array containing the dot product of the M
rows of A with B. Applied to our example, the dot product of the room
matrix with the cost vector yields the costs of the 5 rooms. That is, we
apply the cost vector to each of the room vectors and produce a vector
containing the furnishing costs of the 5 rooms.
print("Room furnishings\n", room_matrix)
print("Furniture cost vector\n",cost_vector)
print("Room costs vector\n",room_matrix.dot(cost_vector))
Room furnishings
[[ 6 3 4 1]
[ 5 2 3 2]
[ 8 3 6 2]
[ 2 1 3 5]
[10 4 7 2]]
Furniture cost vector
[ 40 175 90 450]
Room costs vector
[1575 1720 2285 2775 2630]
The mathematical name for what python calls the dot method is
matrix multiplication.
As is often the case in Python, important binary operations that can be
computed with a method can also be computed using an operator. Following
the convention of arithmetic operators like + and -, the
operator is written between its two arguments. The operator symbol for
matrix multiplication is @, so the matrix multiplication above can
also be written:
print(room_matrix @ cost_vector)
[1575 1720 2285 2775 2630]
6.1.3. Arrays as Data Types¶
numpy ndimensional-arrays are a new data type to be added to our
list of Python data types. Like other data types, they have their list
of type-specific attributes.
Line 1 of the cell below shows room_matrix has shape (5,4),
meaning it has two dimensions, a row dimension and a column dimension,
and the size of the row dimension is 5 and the size of the column
dimension is 4. Line 2 shows it is a 2D array (ndim = 2). Line 3
shows that the type of each entry is np.int64 a numpy-internal
data type for integers. Line 4 shows how much memory each element of the
array takes up (in bytes). Line 6 shows the official numpy-internal
data type for 2 dimensional arrays is np.ndarray. That is, 1D arrays
2D arrays and higher dimensional arrays all belong to the same type.
print(room_matrix.shape)
print(room_matrix.ndim) # a is a 2D array
print(room_matrix.dtype.name) # np.int64 maxint = 2**63 - 1
print(room_matrix.itemsize) # Such an int takes up 8 bytes of memory
print(room_matrix.size) # Number of elements
print(type(room_matrix))
(5, 4)
2
int64
8
20
<class 'numpy.ndarray'>
The python interpreter and the print function will print out arrays
differently (Although this is an option any Python type can take, most
types look the same whether they’re printed by print or the
interpreter). Either way, arrays look different from lists.
# b is an array created from a list
L = [6, 7, 8]
b = np.array(L)
# print the list
print(L)
# print the array
print(b)
# This cell returns the array
b
[6, 7, 8]
[6 7 8]
array([6, 7, 8])
A sequence of sequences can be used to define a 2D-array, but since the inner sequences are rows, they must all be the same length.
import numpy as np
b = np.array( [ (1.5,2,3), (4,5,6) ] )
b
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
This is what we did to define row_matrix above.
Arrays can also contain complex numbers, an important property if they are to serve as the computational versions of matrices in mathematics. Matrices with complex numbers have important applications, for example, in quantum mechanics. However, we won’t be making much use of this feature in this course.
c1 = np.array( [ [1+1j,2-3j], [3+5j,4+1j] ])
c2
array([[1.+1.j, 2.-3.j],
[3.+5.j, 4.+1.j]])
As with real numbers, arrays with complex numbers can be decomposed into their real and imaginary parts:
R = np.array([[1,2],[3,4]])
I = np.array([[1,-3],[5,1]])
c2 = R + 1j*I
c2
array([[1.+1.j, 2.-3.j],
[3.+5.j, 4.+1.j]])
print(R.dtype,I.dtype,c2.dtype)
int64 int64 complex128
6.1.4. Creating a new array ( np.zeros( ) )¶
A very convenient way to fill an array is to start with an array containing all 0’s or 1’s and then update the contents:
X = np.zeros( (3,4) )
X
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
The corresponding function for ones is np.ones().
np.ones( (3,4) )
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
For a discussion of the Python builtin function range, see the
range_and_enumerate_in_python notebook. For now we note that its
most frequent use is to take an integer argument n and return an
iterable range of numbers from 0 throgh n-1.
This provides a convenient way to write a loop filling an array with values.
rows,cols = (3,4)
X = np.zeros((rows,cols))
for i in range(rows):
for j in range(cols):
X[i,j] = i+j
X
array([[0., 1., 2., 3.],
[1., 2., 3., 4.],
[2., 3., 4., 5.]])
6.1.5. Reshaping an array¶
A.reshape((m,n))
means recasting the data in and A into m rows and n columns., This
means A has to have m x n cells. Reshaping can be done on any array
that has the right number of cells. For example, a 2D 3x4 array can be
reshaped into a 6x2 array.
Y = np.arange(12).reshape((3,4))
print(Y,end="\n\n")
print(Y.reshape((6,2)))
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[ 0 1]
[ 2 3]
[ 4 5]
[ 6 7]
[ 8 9]
[10 11]]
6.1.6. Indexing 2D arrays¶
Let’s take a closer look at how arrays are indexed.
We saw above that indexing 1D arrays works exactly like indexing lists.
Indexing 2D arrays works similarly, except that now there are two dimensions to worry about.
print(X)
X[0,3] # first row, fourth col
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
3.0
print(X)
X[1,2] # second row, third col
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
3.0
Exercise
Here is X again.
print(X)
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
Without executing the cell try to predict what value will be returned by the command below. Then check your answer. What happened and why?
X[3,0]
X[3,0]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_96740/1799334490.py in <module>
----> 1 X[3,0]
IndexError: index 3 is out of bounds for axis 0 with size 3
This expression raises an IndexError because it tries to access the
fourth row of X and X has no fourth row. Notice that we accessed
X[0,3] with no problem above, so that maximum index that can be used
for a dimension depends on the size of that dimension. X has shape
X.shape
(3, 4)
so the maximum index in the row dimension is 2 and the maximum index in he column dimension is 3.
6.1.7. Indexing 2D arrays, 2D Slices¶
Using a_1D and a as defined above, we review 1D and 2D value
retrieval:
a_1d = np.arange(15)
a = np.arange(15).reshape(3, 5)
print(a)
a_1d[13]
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
13
print(a)
a[2,3]
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
13
Now let’s retrieve an entire subpart of array.
Here’s an expression that returns the third row of a as a 1D array:
a[2,:]
array([10, 11, 12, 13, 14])
An expression that returns a splice (the first two items) of the third
row of a as a 1D array:
a[2,0:2]
array([10, 11])
Further examples to study.
import numpy as np
X = np.arange(10,130,10).reshape((3,4))
X
array([[ 10, 20, 30, 40],
[ 50, 60, 70, 80],
[ 90, 100, 110, 120]])
fill_val = 20
print(X)
print('-'*fill_val) # ---------------
print(X[2,3]) # value in 3rd row, 4th col.
print('-'*fill_val) # ---------------
print(X[2,:]) # entire 3rd row
print('-'*fill_val) # ----------------
print(X[:,2]) # entire 3rd col; note it still prints horizontally
print('-'*fill_val) # -----------------
print(X[1:3,1:3]) # a sub array of X, also 2D
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
--------------------
120
--------------------
[ 90 100 110 120]
--------------------
[ 30 70 110]
--------------------
[[ 60 70]
[100 110]]
Note that rows and columns both print out horizontally. This is because both are 1D arrays. Python 1D arrays don’t support a distinction between being row vectors and column vectors, because they lack the second dimension the distinction requires.
This is consistent with mathematical usage; the first class citizens of
an 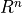 vector space are simply n-tuples of numbers; there is
no additional dimension distinguishing row n-tuples from column
n-tuples.
vector space are simply n-tuples of numbers; there is
no additional dimension distinguishing row n-tuples from column
n-tuples.
A distinction between row and column vectors can be introduced by reshaping.
print(X[2,:])
print(X[2,:].reshape((1,4)))
print(X[2,:].reshape((4,1)))
[ 90 100 110 120]
[[ 90 100 110 120]]
[[ 90]
[100]
[110]
[120]]
But then we have 2D arrays (note the extra brackets).
Another set of examples.
# This cubes every element of np.arange(10)
a = np.arange(10)**3
a
array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729])
Look at the shape of an array to confirm how many dimensions it has:
a.shape
(10,)
This is a 1D array, so it has only one shape number and a single cell is indexed by a single index.
a[2]
8
Attempting to access a 1D array with two indices is an IndexError:
a[2,0]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_83202/1031093193.py in <module>
----> 1 a[2,0]
IndexError: too many indices for array: array is 1-dimensional, but 2 were indexed
So as a first approximation,indexing arrays works much as indexing lists does, with the proviso that multiple indexes are needed for arrays with more than one dimension.
Some observations about slicing with 2D arrays using Y as defined
below for an example.
Y = np.arange(10,160,10).reshape((3,5))
All conventions for slicing numpy arrays are inherited from Python
slicing conventions): The following expression gives the second row of
our 2D array Y
Y[1,:]
The following expression gives the 3rd column of Y:
Y[:,2]
The following expression gives a complete copy of Y
Y[:,:]
As a convenience, numpy lets you skip the : when you want a row.
In other words, the next two expressions are synonyms. Note that you
need the : if you want a column.
print(Y[1,:])
print(Y[1])
[ 60 70 80 90 100]
[ 60 70 80 90 100]
print(X, end="\n\n")
print(X[1,:], X[1,:].shape) # Row. a 1D array
print(X[:,1], X[:,1].shape) # Col. a 1D array
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
[1. 2. 3. 4.] (4,)
[1. 2. 3.] (3,)
Now let’s get a 2x2 subarray, consisting of the upper left hand corner
of X, followed by the central part of the last two rows.
print(X)
print(X[:2,:2])
print(X[1:,1:3])
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
[[10 20]
[50 60]]
[[ 60 70]
[100 110]]
All rows and every other column (uses the “step” argument of a slice with the value 2):
print(X,end="\n\n")
print(X[:,::2])
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
[[0. 2.]
[1. 3.]
[2. 4.]]
All rows and every other column, starting at the second column.
print(X,end="\n\n")
print(X[:,1::2])
[[0. 1. 2. 3.]
[1. 2. 3. 4.]
[2. 3. 4. 5.]]
[[1. 3.]
[2. 4.]
[3. 5.]]
Every other row and every other column, starting at the second column.
print(X[::2,1::2])
[[ 20 40]
[100 120]]
6.1.8. Exercise¶
Use array V defined in the next cell. Write expressions to find the
given slices of V.
a. b.
array([[550, 600], array([550, 600])
[750, 800]])
c. d.
array([[300, 350], array([[300, 350],
[500, 550], [700, 750]])
[700, 750],
[900, 950]])
e.
array([[250, 350],
[650, 750]])
V = np.arange(50,1250,50).reshape((6,4))
V
array([[ 50, 100, 150, 200],
[ 250, 300, 350, 400],
[ 450, 500, 550, 600],
[ 650, 700, 750, 800],
[ 850, 900, 950, 1000],
[1050, 1100, 1150, 1200]])
V[2:4,2:4]
array([[550, 600],
[750, 800]])
V[2:3,2:4]
array([[550, 600]])
V[1:5,1:3]
array([[300, 350],
[500, 550],
[700, 750],
[900, 950]])
V[1:5:2,1:3]
array([[300, 350],
[700, 750]])
V[1:5:2,::2]
array([[250, 350],
[650, 750]])
6.1.8.1. Transposition and Shape¶
The shape of an array is a fixed property, but we can use the data in an array to create a new array with a different shape.
After reshaping, the original array retains its original shape, and can only be indexed according to its original shape:
Y = np.arange(12).reshape((3,4))
Z = Y.reshape((4,3))
print("Z\n",Z)
print("Y\n",Y)
print("Y[2,3]\n",Y[2,3])
print("Z[3,2]\n",Z[3,2])
print("Y[3,2]")
print(Y[3,2])
Z
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
Y
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
Y[2,3]
11
Z[3,2]
11
Y[3,2]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[45], line 8
6 print("Z[3,2]\n",Z[3,2])
7 print("Y[3,2]")
----> 8 print(Y[3,2])
IndexError: index 3 is out of bounds for axis 0 with size 3
However, the two arrays Z and Y still share the same data.
We say that Z and Y are view of the same data. What that
means is that changing Z also changes Y (and also vice versa):
print('Y:\n', Y)
print('Z:\n', Z)
print(' Y[1,0] = 14 ==>')
Y[1,0] = 14
print('Y\n', Y)
print('Z:\n', Z)
Y:
[[ 0 1 2 14]
[ 4 5 6 7]
[ 8 9 10 11]]
Z:
[[ 0 1 2]
[14 4 5]
[ 6 7 8]
[ 9 10 11]]
Y[1,0] = 14 ==>
Y
[[ 0 1 2 14]
[14 5 6 7]
[ 8 9 10 11]]
Z:
[[ 0 1 2]
[14 14 5]
[ 6 7 8]
[ 9 10 11]]
Another view of the same data is obtained by transposition.
Array transposition is sometimes a nice way to get to the 2D array you
really want. The transposition of an array M is called M.T, and
the definition is that
M.T[i,j] = M[j,i]
So if M is an m x n array, then M.T is an n x m
array. Look at X.T and verify these observations. The mth row
of X becomes the mth column of X.T. The nth column
of X becomes the nth row of X.T.
Note that transposition can change the shape of an array.
X = np.arange(10,130,10).reshape((3,4))
print("X\n", X,"\n",X.shape)
print()
T = X.T
print("X.T\n", T,"\n",T.shape)
print()
print("X[1,2]\n",X[1,2], "\nX.T[2,1]\n",T[2,1])
X
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
(3, 4)
X.T
[[ 10 50 90]
[ 20 60 100]
[ 30 70 110]
[ 40 80 120]]
(4, 3)
X[1,2]
70
X.T[2,1]
70
As with reshaped arrays, transposition gives a new array but one that shares the same data, so that changing the transposed array also changes the original.
T[1,2] = 14
print(T)
print()
print(X)
[[ 10 50 90]
[ 20 60 14]
[ 30 70 110]
[ 40 80 120]]
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 14 110 120]]
6.1.8.2. Assigning to slices (broadcasting)¶
Now in general 1D arrays are very like lists, but it is important to note that assignment works a little differently with arrays.
a = np.arange(10)**3
print(a)
a[2:5]
[ 0 1 8 27 64 125 216 343 512 729]
array([ 8, 27, 64])
A big difference between an array and a list is that arrays allow scalar
assigments to slices. If the assignee slice is greater than 1x1, the
assignment is “broadcast” to each of the cells in the slice (we discuss
broadcasting in more detail in another numpy notebook).
In the next cell we demonstrate assignment to a slice. In standard Python the value that is assigned to a slice has to be a sequence. But in numpy it is treated as an elementwise operation, so in the next example, we assign the value 5 to each of the positions in the splice.
Note that how many 5s there are in the result is determined by the
length of the splice a[3:6], so the length of the assignee array
a remains unchanged by the assignment.
a = np.arange(10)**3
print(len(a), a)
print(a[3:6])
a[3:6] = 5
print(len(a), a)
10 [ 0 1 8 27 64 125 216 343 512 729]
[ 27 64 125]
10 [ 0 1 8 5 5 5 216 343 512 729]
An example using a slice with a “step”-size of 2
print(a)
print(a[0:6:2])
a[0:6:2] = -1000
print(a)
[ 0 1 8 5 5 5 216 343 512 729]
[0 8 5]
[-1000 1 -1000 5 -1000 5 216 343 512 729]
Note again: the length of the array did not change, despite the fact
that we were assigning a sequence of length 1 to a span of length 3 in
a. To accommodate the assignment, the value -1000 is “broadcast”
over the specified span of a.
This a key difference from how standard Python sequence assignment works. There is no “broadcasting” behavior. Instead, the assignee sequence is shortened.
L = list(range(10))
print(len(L), L)
L[2:4] = [5]
print(len(L), L)
10 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
9 [0, 1, 5, 4, 5, 6, 7, 8, 9]
The bottom line is that in a numpy assignment the length – more generally, the shape – of the assignee never changes.
If numpy can’t figure out how to broadcast the assignment to
preserve shape, it raises an Exception.
a = np.arange(10)**3
print(len(a), a)
a[2:5] = [5,6]
print(len(a), a)
10 [ 0 1 8 27 64 125 216 343 512 729]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Input In [270], in <cell line: 3>()
1 a = np.arange(10)**3
2 print(len(a), a)
----> 3 a[2:5] = [5,6]
4 print(len(a), a)
ValueError: could not broadcast input array from shape (2,) into shape (3,)
The rules governing what shape mismatches work in assignment are known as the rules of broadcasting. They are discussed in some slides and another notebook.
For now we content ourselves with a more complicated example, in which the shape of the assignee slice is 2D, but assigning a 1D value still works.
b = np.arange(20).reshape((5,4))
print("b\n", b,end="\n\n")
print("b[1:3,1:3]\n", b[1:3,1:3],end="\n\n")
val = 20*np.ones((2,))
print("Val\n",val,end="\n\n")
b[1:3,1:3] = val
print("b\n", b,end="\n\n")
print("b slice\n", b[1:3,1:3],end="\n\n")
b
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]]
b[1:3,1:3]
[[ 5 6]
[ 9 10]]
Val
[20. 20.]
b
[[ 0 1 2 3]
[ 4 20 20 7]
[ 8 20 20 11]
[12 13 14 15]
[16 17 18 19]]
b slice
[[20 20]
[20 20]]
6.1.9. Three-D (and more) arrays¶
There are also 3D arrays, which have a third dimension; each position along the third dimension defines a 2D array.
A =np.arange(24).reshape((2,3,4))
A
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
Think of the array beginning with 12 as a layer lying “underneath” the array beginning with 0.
In a 2D array, a single index slice is a row or column (a 1D array). In a 3D array, a single index slice is a 2D array.
print(A)
A[1,:,:]
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
array([[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
A[1,:,:] is the second layer.
The next slice slices off the last columns of the two layers.
print(A)
A[:,:,3]
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
array([[ 3, 7, 11],
[15, 19, 23]])
The next slice slices off the last rows of the two layers.
print(A)
A[:,2,:]
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
array([[ 8, 9, 10, 11],
[20, 21, 22, 23]])
And here is an array consisting of the upper left hand corners of the two layers.
A[:,0,0]
array([ 0, 12])
We will not be using 3D arrays much, and they will not be featured on tests. But it’s nice to know they’re out there.
An easy example of where you might want a 3D array is a color image.
Specifying each pixel position in the image takes two numbers, and in a
black and white image we can just have the cell at that position contain
a single number representing the grayscale magnitude. But for a color
image we need three numbers, and it is very convenient for many purposes
to use a third dimension for those three numbers; for example, using the
third dimension for the color, and the first “layer” in the 3rd
dimension for red, there is an easily retrievable 2D array representing
all the “red” values for the image I:
I[:,:, 0]
In machine learning applications, especially in deep learning applications, 3D arrays and higher are not at all uncommon. One reason is that it is very convenient (and efficient) to use one dimension for the batch number. Another is that words in the input are often represented as “vectors” (1D arrays of floating point numbers). Then
D[22, 12,:]
retrieves the word vector for the 13th word in the 23rd batch.
6.2. Elementwise arithmetic operations and broadcasting¶
We can add arrays M and N of the same shape.
M+N[i,j] = M[i,j] + N[i,j]
The operation is pretty intuitive.
import numpy as np
a = np.array( [20,30,40,50] ).reshape((2,2))
b = np.arange( 4 ).reshape((2,2))
print(a)
print(b)
[[20 30]
[40 50]]
[[0 1]
[2 3]]
a + b
array([[20, 31],
[42, 53]])
This is known as elementwise arithmetic.
It extends to other arithmetic operations beside addition.
a * b
array([[ 0, 30],
[ 80, 150]])
a - b
array([[20, 29],
[38, 47]])
Exercise
Add 1 to every element of the the array Q by creating a new array of
the right shape containing only 1s (use np.ones, which works like
np.zeros) and adding the two arrays.
Q = np.arange(0,24,2).reshape((3,4))
Q
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
Demonstrating np.ones().
np.ones((2,4))
array([[1., 1., 1., 1.],
[1., 1., 1., 1.]])
print(Q)
print(Q + np.ones((3,4)))
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]]
[[ 1. 3. 5. 7.]
[ 9. 11. 13. 15.]
[17. 19. 21. 23.]]
print(Q)
print(Q + np.ones((3,4),dtype=int))
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]]
[[ 1 3 5 7]
[ 9 11 13 15]
[17 19 21 23]]
In the next example we illustrate simple broadcasting with arithmetic operations. We were briefly introduced to broadcasting above for the case of assignment.
The simplest case of broadcasting with arithmetic operations is when
elementwise operations apply between arrays and scalars (ordinary
numbers). So for example, 2 * a (where a is the array above)
returns an array that contains all the elements of a multiplied by
2.
print(a)
print()
print(2 * a)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14]
[ 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28]
This works by “broadcasting” 2 into an array the same size as a
and then doing elementwise mutliplication on the two arrays.
We will say more about broadcasting in a subsequent notebook.
Exercise
The same as the last exercise: Add 1 to every element of the the array
Q. Only this time, do it by adding a scalar value to Q.
Q = np.arange(0,24,2).reshape((3,4))
Q
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
print('Q\n',Q)
print()
print('Q+1\n',Q+1)
Q
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]]
Q+1
[[ 1 3 5 7]
[ 9 11 13 15]
[17 19 21 23]]
Exercise
Create an array QP which contains 2 raised to every power contained in Q:
![\text{QP[i,j]} = 2^{\text{Q}[i,j]}](../_images/math/4e2eab2530836cefa1c70e62f5f32a354cf2d7bf.png)
Q
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
So for example, since Q[2,3] is
Q[2,3]
22
QP[2,3] should be
## Note this is the general syntax for a to the b power (a**b)
2**22
4194304
QP = 2**Q
QP
array([[ 1, 4, 16, 64],
[ 256, 1024, 4096, 16384],
[ 65536, 262144, 1048576, 4194304]])
QP[2,3]
4194304
6.3. More broadcasting¶
A more complicated case is when we have two arrays of different shape,
one s of shape 2x3 and the other t, a 1D array of length 3.
![s =
\left \lbrack
\begin{array}{ccc}
0 & 1 & 2\\
3 & 4 & 5
\end{array}\right \rbrack\\
t =
\left \lbrack
\begin{array}[t]{ccc}
0 & 1& 2\\
\end{array}\right \rbrack\\](../_images/math/aa3b75f43f72ee46cd7722cd3512b2c84f684e15.png)
and we broadcast t to be 2x3 to match s.
![\left \lbrack
\begin{array}[t]{ccc}
0 & 1& 2\\
\end{array}\right \rbrack
\Rightarrow
\left \lbrack
\begin{array}{cccc}
0 & 1& 2\\
0& 1 & 2
\end{array}
\right \rbrack](../_images/math/2bdc2870e47aba89f17e2ac7fb4bf3484fae9779.png)
Then we do elementwise arithmetic to compute 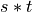 .
.
s = np.arange(6).reshape((2,3))
t = np.arange(3)
print("s\n",s)
print()
print("t\n",t)
print()
u = s * t
print("u = s * t\n",u)
s
[[0 1 2]
[3 4 5]]
t
[0 1 2]
u = s * t
[[ 0 1 4]
[ 0 4 10]]
The result is a new array  whose
whose 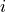 th column is the
result of multiplying the
th column is the
result of multiplying the 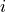 th colum of
th colum of  (
(![s[:,i]](../_images/math/b3f5630194c1406789e55c6e1845f35f8adff996.png) ) by the
) by the 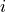 th element of
th element of 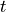 .
.
Of course, you can’t always rely on broadcasting to figure out what to
do with all mismatched array sizes. In general, multiplying arrays of
different sizes together will fail with a ValueError that announcing
that broadcasting failed:
c = np.array([3,2,1,5,4])
print(f'a ({a.shape[0]:<2}, ) {a}')
print(f'c ({c.shape[0]:<2}, ) {c}')
a * c
a (10, ) [ 0 1 8 27 64 125 216 343 512 729]
c (5 , ) [3 2 1 5 4]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[63], line 4
2 print(f'a ({a.shape[0]:<2}, ) {a}')
3 print(f'c ({c.shape[0]:<2}, ) {c}')
----> 4 a * c
ValueError: operands could not be broadcast together with shapes (10,) (5,)
Exercise
Look at the array Q defined in the next cell.
Create a new array that is just like Q except that the values in
Q’s first column are multiplied by 2, the values in Q’s
second column are multiplied by 4, the values in Q’s third column
are multiplied by 8, and the values in Q's 4th columns are
multiplied by 16
Q = np.arange(0,24,2).reshape((3,4))
Q
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
#Answer 1
print(Q)
print()
print(Q * np.array([2,4,8,16]))
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]]
[[ 0 8 32 96]
[ 16 40 96 224]
[ 32 72 160 352]]
# Answer 2
print(Q)
print()
powers = 2**np.arange(1,5)
print(powers)
print()
print(Q * powers)
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]]
[ 2 4 8 16]
[[ 0 8 32 96]
[ 16 40 96 224]
[ 32 72 160 352]]
Exercise. Produce a 2-column array whose first column contains the
result of adding the first two columns of X (defined above) and
whose second column contains the result of adding the last two columns
of X.
In others words, sinc e X is
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
the result we want is:
array([[ 30, 70],
[110, 150],
[190, 230]])
Hint: this can be done in a single step with by adding two distinct
slices of X. Th slices will will involve using a step-size otehr
than one.
Reviewing step-slicing on a different exampl:
Q
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
Q[:,::2]
array([[ 0, 4],
[ 8, 12],
[16, 20]])
Q[:,1::2]
array([[ 2, 6],
[10, 14],
[18, 22]])
print(X)
print(X[:,::2])
print(X[:,1::2])
print()
X[:,::2] + X[:,1::2]
[[ 10 20 30 40]
[ 50 60 70 80]
[ 90 100 110 120]]
[[ 10 30]
[ 50 70]
[ 90 110]]
[[ 20 40]
[ 60 80]
[100 120]]
array([[ 30, 70],
[110, 150],
[190, 230]])
The next example illustrates an idea closely related to elementwise arithmetic, the idea of a universal function (or ufunc).
This term refers to a function that is fundamentally numerical but which
can be applied to an array of numbers; the application of the function
to an array is interpreted as elementwise application of the function.
For example, where 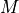 is a 2D array,
is a 2D array,
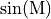
denotes a 2D array such that
![\sin(\text{M})[i,j] = \sin(M[i,j]).](../_images/math/2d592f4b8a80dc9b1dfe66336f3b668414773321.png)
# For next problem
#SQUARE ROOT OF 3 DIVIDED BY 2
print(f"{(3**.5)/2:.8e}")
8.66025404e-01
We take the sin of an array consisting of 0, 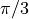 ,
,
 , and
, and 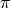 .
.
The takeaway here is that we get the result of applying np.sin to
each of the numbers in the array.
That should be an array containing  and
and  .
.
And it is, given that we’re computing with a computer.
Note that the last value in the result is just a very a tiny float
(order 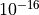 ).
).
a = np.arange(0,(4/3)*np.pi,np.pi/3)
print("a\n",a)
print("sin(a)\n",np.sin(a))
a
[0. 1.04719755 2.0943951 3.14159265]
sin(a)
[0.00000000e+00 8.66025404e-01 8.66025404e-01 1.22464680e-16]
On this case we say the function is vectorized, that is generalized from a function that applies to numbers to a function that applies to vectors of numbers (in fact, any array of numbers, 1D, 2D, and beyond).
Ass noted above, such functions are also called Ufuncs (or universal functions) in numpy.
The next example combines the idea of scalar multiplication of arrays
with a universal function We apply two operations to a: first
sin, then multiplication by 10.
10*np.sin(a)
array([0.00000000e+00, 8.66025404e+00, 8.66025404e+00, 1.22464680e-15])
6.4. Boolean operations¶
One extremely important application of the idea of a vectorized operation is Boolean conditions or tests.
In numpy, all Boolean conditions are vectorized. Applying a Boolean
condition to an array results in an array of Booleans, computed by
applying the condition to each of the elements of the array.
a = np.arange(0,50,10)
print(a)
Y = a < 35
print(Y)
[ 0 10 20 30 40]
[ True True True True False]
The usefulness of Boolean arrays is that a Boolean array can be used to index an array of the same shape. The value of such an expression is the array of elements for which the Boolean array is True:
# All the elements of a that are less than 35
a[Y]
array([ 0, 10, 20, 30])
Note the shape of a[Y] differs from the shape of a; in general
the number of elements returned when indexing an array a with a
Boolean condition is determined by the number of elements of a
satisfying the condition.
A shorter version of what we just did:
a[a < 35]
array([ 0, 10, 20, 30])
This is the idiomatic way of saying: The members of a less than 35.
Applying a Boolean array to select members of another array is called
Boolean masking or Boolean indexing. It is called Boolean
masking the Boolean array masks over the undesired values and lets
through only those matched by a True. It is called Boolean indexing
because the Boolean array serves much the same purpose as a sequence of
indexes picking out multiple values (see fancy indexing below).
Another kind of Boolean test is ==.
Consider
a = np.arange(0,50,10)
a[1] = 20
print(a)
b = np.arange(-20,80,20)
b[-1] = 40
print(b)
print(a == b)
[ 0 20 20 30 40]
[-20 0 20 40 40]
[False False True False True]
Boolean tests on arrays will raise an error if applied in a context that requires a single ambiguous Boolean result:
a = np.arange(0,50,10)
print(a)
b = np.arange(-20,80,20)
print(b)
if a == b:
print("Hi!")
[ 0 10 20 30 40]
[-20 0 20 40 60]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_44470/1813055576.py in <module>
3 b = np.arange(-20,80,20)
4 print(b)
----> 5 if a == b:
6 print("Hi!")
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
Of course the result of this Boolean test is not True or False.
a==b
array([False, False, True, False, False])
This is what Python means by saying “The truth value of an array with more than one element is ambiguous.” Generally it’s a mixture of truths and falsities, like real life.
What can be used as a test is to ask if any of the Boolean results is true, or if all of them are.
For example:
# Implementing one of the suggested fixes. Change (a == b).any() to (a == b).all()
# For a different result.
if (a == b).any():
print("Hi!")
Hi!
a.all() requires all the Booleans be True and can also serve the
purposes of converting a Boolean vector toa single truth-value.
(a==b).all()
False
6.4.1. Elementwise Boolean operations, Masking¶
Let’s look more closely at using Boolean arrays as masks.
Reviewing the principle: Applying a Boolean test to an array returns an array of truth-values: Just as
3 + X
adds 3 to every element of array X, so
X > 2
returns an array of truth-values which tells us which elements of X
are greater than 2.
import numpy as np
X = np.array([1,5,2,7,9,4,3,-6])
print(X)
print(X >= 3)
[ 1 5 2 7 9 4 3 -6]
[False True False True True True True False]
As we saw above, Boolean arrays can be used to index other arrays. They must be the same shape as the array they index. So in the simplest case:
print(X)
print(X[np.array([False, True, False, True, True, True, True, False])])
[ 1 5 2 7 9 4 3 -6]
[5 7 9 4 3]
But X>=3 is a Boolean array is a Boolean array of exactly the right
shape to index X. Hence we can use it as a mask to produce an array
consisting of exactly the members of X that are greater than or
equal to 3.
print(X)
print(X>=3)
print(X[X>=3])
[ 1 5 2 7 9 4 3 -6]
[False True False True True True True False]
[5 7 9 4 3]
We can achieve the same result with a list comprehension, but the array computation above is much faster:
np.array([x for x in X if x >= 3])
array([5, 7, 9, 4, 3])
Boolean arrays can also be used to count the number of elements in
an array that satisfy some constraint. Although len works on arrays
and could be used, sum is faster. The Boolean True is treated as
1 and the Boolean False as 0, so summing a Boolean array counts the
number of occurences of True.
Therefore following expression, labeled “Solution A”, correctly counts
the number of elements in X that are greater than or equal to 3.
print("Solution A")
(X>=3).sum()
Solution A
5
Notice that Solution A does not have X[X>=3] as part of it; on the
other hand, Solution B, which follows, does.
print("Solution B")
len(X[(X>=3)])
Solution B
5
Solution B computes the list of elements greater than 3, then measures its length. Solution A computes a list Booleans, never collects the actual list of numbers, then adds Booleans.
So far we have Boolean constraints can also be used to index along one dimension at a time.
In the next cell, we use Boolean constraints on the just the row
dimension to pick out the first, third, and fourth rows of array U.
In this case, since U is 5x6, the Boolean array must have size 5.
U = np.arange(0,300,10).reshape((5,6))
print(U)
U[[True,False,True,True,False],:]
[[ 0 10 20 30 40 50]
[ 60 70 80 90 100 110]
[120 130 140 150 160 170]
[180 190 200 210 220 230]
[240 250 260 270 280 290]]
array([[ 0, 10, 20, 30, 40, 50],
[120, 130, 140, 150, 160, 170],
[180, 190, 200, 210, 220, 230]])
Exercise
In the cell below we define X, a 2x4 array. Use a Boolean mask to
return first, second and fourth columns of X.
import random
def select_S (S,R):
"""
Select S random ints from the given by R
"""
return np.array([random.randrange(0,R) for i in range(S)])
seed=47
random.seed(seed)
X = select_S(8,20).reshape((2,4))
print(X)
[[11 2 13 17]
[14 18 10 8]]
X[:,[True,True,False,True]]
array([[11, 2, 17],
[14, 18, 8]])
6.4.1.1. “Fancy” indexing¶
Cook up a sequence consisting of the indices of the first, third, and seventh elements of an array, namely:
[0,2,6]
Now use that sequence as a fancy index on X to retrieve the
first third and seventh elements of X.
print(X)
X[[0,2,6]]
[ 1 5 2 7 9 4 3 -6]
array([1, 2, 3])
So what is fancy indexing? Fancy indexing is using a sequences of indexes to return a sequence of values. The sequence of indexes can be any sequence, a list, a tuple, an array.
Note that the option of doing fancy indexing has nothing to do with how many dimensions the array has. In this example, we used a 1D array X and passed in a sequence to retrieve 3 different values along one dimension.
So watch out for the difference between fancy indexing and indexing along multiple dimensions.
![\begin{array}{l|l|l}
\text{Task} & \text{Syntax} & \text{Returns}\\
\hline
\text{Fancy indexing} & X[[0,2,6]] & \text{A sequence of layers (3D array), rows (2D array), or values (1D array)}\\
\text{Indexing multiple dimensions} & X[0,2,6] & \text{One value from a 3D array} \text{ Error from 1D or 2D array}\\
\end{array}](../_images/math/0fc5a2927376574cf3c908e440e8e1396c7432e2.png)
If we mean to fancy index but leave out a pair of brackets, that’s
interpreted as an attempt to index 3 dimensions of X, which is an
error if X is not a 3D array.
Since our current X is a 1D array, this is an error.
X[0,2,6]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
/var/folders/w9/bx4mylnd27g_kqqgn5hrn2x40000gr/T/ipykernel_24934/1606959147.py in <module>
----> 1 X[0,2,6]
IndexError: too many indices for array: array is 1-dimensional, but 3 were indexed
X
array([ 1, 5, 2, 7, 9, 4, 3, -6])
Fancy indexing can be done along any one of an array’s dimensions, and multiple dimensions can be fancy-indexed at the same time, though the fancy sequences must then be of the same length.
The following fancy-indexing expression returns three values from Y,
the value at [0,1], [0,3], and [2,2].
So the pattern for 2D fancy indexing is
X[row_indices,column_indices].
Y = np.arange(12).reshape((3,4))
print(Y)
print()
print(Y[[0,0,2],[1,3, 2]])
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[ 1 3 10]
Below we use fancy indexing to permute the rows and columns of a 3x7 array.
WW =np.arange(21).reshape((7,3))
print(WW)
print()
WW_swap_rows = WW[[1,2,0,6,4,3,5],:]
print(WW_swap_rows)
print()
WW_swap_columns = WW_swap_rows[:,[1,0,2]]
print(WW_swap_columns)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]
[15 16 17]
[18 19 20]]
[[ 3 4 5]
[ 6 7 8]
[ 0 1 2]
[18 19 20]
[12 13 14]
[ 9 10 11]
[15 16 17]]
[[ 4 3 5]
[ 7 6 8]
[ 1 0 2]
[19 18 20]
[13 12 14]
[10 9 11]
[16 15 17]]
We use fancy indexing to randomly sample from an array’s values:
import random
# A random sample of S values from WW
N = 10
W =np.arange(21)
R,C = WW.shape
def select_N (N,R):
"""
Select S random ints from the range given by R
"""
return np.array([random.randrange(0,R) for i in range(N)])
# Change this to get a new sample
seed=12
random.seed(seed)
# We sample S=10 values from W, the 1D array, using
# the length of the array to define the range we select
# indices from.
# Note that this is sampling with replacement (11 sampled twice)
W[select_N(N,21)]
array([15, 8, 16, 11, 4, 12, 0, 11, 15, 8])
Your next task is to extend the example above by using select_S to
select exactly S=10 values from the 2D array WW defined above and
reprinted in the next cell. Be sure that all 10 values are independent
of each other. For example you should neither avoid nor be biased toward
having values in the same row.
Beyond the independence issue, note that if you only select rows you
will get 30 values, not 10, because there are 3 columns. If you select 3
rows you will get 9 values and if you select 4 you will get 12. The game
is to use select_S to get exactly 10.
print("WW\n",WW)
# Change this to get a new sample
seed=47
random.seed(seed)
WW
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]
[15 16 17]
[18 19 20]]
In correct answer selecting 10 rows:
# Here N=10 and R is the number of rows in WW
WW[select_N(N,R)]
array([[15, 16, 17],
[18, 19, 20],
[ 9, 10, 11],
[15, 16, 17],
[18, 19, 20],
[12, 13, 14],
[ 3, 4, 5],
[12, 13, 14],
[ 0, 1, 2],
[15, 16, 17]])
We need to select row indices as well as column indices using WW’s
shape – RxC – to define the rnages we are selecting from.
WW[select_N(N,R),select_N(N,C)]
array([12, 3, 11, 8, 4, 8, 4, 0, 12, 18])
6.4.2. Boolean Operations on Data: Examples¶
Many python modules that provide data do so in array form. As an example, we load the famous iris data set due to Ronald Fisher, familiar to many who’ve had a statistics class, but also to many who’ve a computer science or machine learning class in which data analysis plays a role.
from sklearn.datasets import load_iris
data = load_iris()
features = data['data']
target = data['target']
The name data has been set to a dictionary.
list(data.keys())
['data',
'target',
'frame',
'target_names',
'DESCR',
'feature_names',
'filename',
'data_module']
In the cell loading the data, the name features is given the value
data['data'], which is a 2D numpy array containing only numbers.
print(features.shape)
print(features.ndim)
print(features.dtype.name)
print(features.size)
print(type(features))
print(features[:10])
(150, 4)
2
float64
600
<class 'numpy.ndarray'>
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]]
The last thing printed is the first 10 rows of features. This array
represents data about irises. Each row represents a different iris and
gives 4 measurements for that exemplar. So there are 150 iris exemplars;
with 4 measurements for each, that’s 600 items of data in the array
(features.size). The data is used for classification studies,
especially classification using multiple features to distinguish more
than 2 classes.
Let’s apply what we’ve just learnt to pick a certain subset of the data. The first number in each row represents the sepal length of that particular iris exemplar (to be demonstrated below).
Find the flowers whose sepal length is exactly 5.
# 1D array: first column
first_col = features[:,0]
print(first_col == 5.0)
print((first_col == 5.0).shape)
[False False False False True False False True False False False False
False False False False False False False False False False False False
False True True False False False False False False False False True
False False False False True False False True False False False False
False True False False False False False False False False False False
True False False False False False False False False False False False
False False False False False False False False False False False False
False False False False False False False False False True False False
False False False False False False False False False False False False
False False False False False False False False False False False False
False False False False False False False False False False False False
False False False False False False False False False False False False
False False False False False False]
(150,)
Note: The Boolean array is a 1D array of length 150, one Boolean for
each row in the data. Any Boolean array of this size can be used to
index the rows, combined with a : to indicate we want all columns.
features[first_col == 5.0,:]
array([[5. , 3.6, 1.4, 0.2],
[5. , 3.4, 1.5, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5. , 3.2, 1.2, 0.2],
[5. , 3.5, 1.3, 0.3],
[5. , 3.5, 1.6, 0.6],
[5. , 3.3, 1.4, 0.2],
[5. , 2. , 3.5, 1. ],
[5. , 2.3, 3.3, 1. ]])
So there are only 10 plants out of 150 that have sepal lengths of exactly 5.
Of course we can do this all in one step, with the same result:
features[features[:,0] == 5.0,:]
array([[5. , 3.6, 1.4, 0.2],
[5. , 3.4, 1.5, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5. , 3.2, 1.2, 0.2],
[5. , 3.5, 1.3, 0.3],
[5. , 3.5, 1.6, 0.6],
[5. , 3.3, 1.4, 0.2],
[5. , 2. , 3.5, 1. ],
[5. , 2.3, 3.3, 1. ]])
Notice that what we’ve returned is a set of rows, and that’s consistent
with how we’ve used the Boolean mask features[:,0] == 5.0. Despite
that, the mask defines a condition on columns: the value in the first
column must be 5,0. So we’re asking for the rows such that their
value in the first column is 5.0.
Since we’re indexing rows here, the : can also be left out:
features[features[:,0] == 5.0]
array([[5. , 3.6, 1.4, 0.2],
[5. , 3.4, 1.5, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5. , 3.2, 1.2, 0.2],
[5. , 3.5, 1.3, 0.3],
[5. , 3.5, 1.6, 0.6],
[5. , 3.3, 1.4, 0.2],
[5. , 2. , 3.5, 1. ],
[5. , 2.3, 3.3, 1. ]])
A more interesting use of Boolean array indexing is to find all the
irises of a particular class, using the target array defined when we
loaded the data; the target array contains the class of each iris in
the data set:
print(type(target))
print(target.shape)
print(set(target))
# Grab the first rows of both arrays
print(features[0], target[0])
# Grab row indexed 90 from both arrays
print(features[90], target[90])
<class 'numpy.ndarray'>
(150,)
{0, 1, 2}
[5.1 3.5 1.4 0.2] 0
[5.5 2.6 4.4 1.2] 1
As the printouts indicate , target is a 1D array (a vector) of
length 150, containing only the values 0,1, and 2. These are the three
classes to which an iris can belong. There are exactly as many entries
in the target array as there are rows in the features array. For
any iris, its row-index in the features array is the index of its
class in the target. Above we printed the features and target class
for irises 0 and 90.
We can take advantage of this structure to find all the irises of class
1 very efficiently. Note that target == 1 is a Boolean array of
length 150.
target==1
array([False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False, False, False, False, False])
Since the size of this Boolean array is exactly the same as the number
of rows in features, we can use it to find the rows in features
that represent irises of class 1:
features[target==1,:].shape
(50, 4)
There are 50 rows whose class is 1; you can verify for yourselves
that are also 50 rows for classes 2 and 3. This is a balanced data set.
Going back to the dictionary we loaded when we loaded the datset, we can find the meanings of our 4 columns:
data['feature_names']
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
So our 4 columns have numerical data on these attributes. The column indexed 0 contains the sepal length measurement for 1 flower in our sample. The column indexed 1 contains sepal width measurements. And so on.
We know there are three classes (0, 1, and 2). We can look up their
names under the 'target_names' key of the dictionary we got when we
loaded the data.
data['target_names']
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
So class 0 represent the iris species setosa, and so on.
Here’s what the entire target array looks like:
data['target']
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
6.4.3. Exercise¶
How many irises are there whose species is 1 and whose sepal length is greater than 5.
Advice: An easy way to do this is to do it in two stages. First find the set of rows of species 1, then use that array to place a condition on the sepal length.
# species 1
features1 = features[target==1,:]
# first col
features1[:,0]
array([7. , 6.4, 6.9, 5.5, 6.5, 5.7, 6.3, 4.9, 6.6, 5.2, 5. , 5.9, 6. ,
6.1, 5.6, 6.7, 5.6, 5.8, 6.2, 5.6, 5.9, 6.1, 6.3, 6.1, 6.4, 6.6,
6.8, 6.7, 6. , 5.7, 5.5, 5.5, 5.8, 6. , 5.4, 6. , 6.7, 6.3, 5.6,
5.5, 5.5, 6.1, 5.8, 5. , 5.6, 5.7, 5.7, 6.2, 5.1, 5.7])
There are 50 flowers belonging to species 1.
len(features1[:,0])
# Boolean condition on first col
features1[:,0] > 5.0
array([ True, True, True, True, True, True, True, False, True,
True, False, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, False, True,
True, True, True, True, True])
# rows satisfying condition
XX = features1[features1[:,0] > 5.0]
It turns out nearly all the flowers of species 1 have sepal length greater than 5.
len(XX)
47
# New smaller data table consisting of those flowers of species 1.
species1 = features[target == 1,:]
print(len(species1))
species1[species1[:,0] > 5.0,:]
print(len(species1[species1[:,0] > 5.0,:]))
50
47
Alternatively
print(species1[:,0] > 5.0)
sum(species1[:,0] > 5.0)
[ True True True True True True True False True True False True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True False True True True True
True True]
47
Now suppose we wanted to just see the sepal lengths (column 0) of the target class 1 irises, and compare them to the sepal lengths of the target class 0 irises, to see if sepal lengths provided a good way of telling the two classes apart. We could sort the values to make comparison by eyeball easier:
col_0_class1 = features[target==1,0]
col_0_class1.sort()
print("Class 1 sepal length\n",col_0_class1)
print()
col_0_class0 = features[target==0,0]
col_0_class0.sort()
print("Class 0 sepal length\n",col_0_class0)
Class 1 sepal length
[4.9 5. 5. 5.1 5.2 5.4 5.5 5.5 5.5 5.5 5.5 5.6 5.6 5.6 5.6 5.6 5.7 5.7
5.7 5.7 5.7 5.8 5.8 5.8 5.9 5.9 6. 6. 6. 6. 6.1 6.1 6.1 6.1 6.2 6.2
6.3 6.3 6.3 6.4 6.4 6.5 6.6 6.6 6.7 6.7 6.7 6.8 6.9 7. ]
Class 0 sepal length
[4.3 4.4 4.4 4.4 4.5 4.6 4.6 4.6 4.6 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9
4.9 4.9 5. 5. 5. 5. 5. 5. 5. 5. 5.1 5.1 5.1 5.1 5.1 5.1 5.1 5.1
5.2 5.2 5.2 5.3 5.4 5.4 5.4 5.4 5.4 5.5 5.5 5.7 5.7 5.8]
And though there is some overlap, we see that there is a tendency for the sepal length values to be higher in class 1 than class 0.
To quantify this idea, we would of course take the mean (or average value). We could also look at which class shows the greater variance for that attribute.
print(f"Class 1 sepal length: Mean {col_0_class1.mean():.3f} Var {col_0_class1.var():.3f}")
print(f"Class 0 sepal length: Mean {col_0_class0.mean():.3f} Var {col_0_class0.var():.3f}")
Class 1 sepal length: Mean 5.936 Var 0.261
Class 0 sepal length: Mean 5.006 Var 0.122
Summing up this part of the discussion of arrays: we’ve just illustrated
one of many methods for computing statistical and numerical properties
for numpy ndimensional arrays. They include .all() and .any()
(which we saw above), as well as .argmax(), .argmin(),
.max(),.mean(),.std(), sum(), and var().
All of these return numerical or Boolean values representing aggregate
properties of the array. Aggregate properties can be opposed to
elementwise properties. It makes sense to take sin() of an array
element by element. It doesn’t make sense to speak of the the
elementwise average of an array.
We have also seen array modification methods like .sort() and
.reshape(). These differ from each other in that .sort()
modifies the array in place (which is why we didn’t need to set a
variable to the result of col_0_class1.sort() above).
We will be using these methods and relying on the distinctions between them throughout.
6.5. Why use arrays?¶
Arrays provide all kinds of indexing convenience for accessing data that is genuinely tabular. Tabular data is data that has good reason for being represented in a table; that is, there is good reason to think of the rows as a unit, and good reason to think of the columns as units. And therefore, there is good reason to think we might want to apply some computational operations to columns and rows. We’ll explore those ideas a bit more in a future assignment.
All kinds of data is fundamentally tabular, as we’ll see. But although
that’s very important, it’s probably not the main reason why so many
scientists, engineers, and data analysts use numpy and other
programming tools like matlab and R that provide tables, or
matrices (the mathematical name for a similar concept), as a
fundamental data structure. The main reason is computational efficiency.
Having a single data structure with predictable types and elementwise
basic arithmetic operations makes it possible to write very efficient
ways of performing more complex operations. The code snippet. below
demonstrates this by providing a timing comparison between two ways of
computing the sum of the squares between 0 and 999 inclusive; the first
is used in computing the variable normal_py_sec, is the ordinary
Python way of computing such a sum: Cook up a container of those
integers, square each of them and sum the result. The second, stored in
the varibale np_sec, uses numpy arrays. This uses the dot
product operation that we discussed above to multiply all the
corresponding elements of two vectors (elemntwise) and sums the result.
Using this precompiled fast math operation we speed the code up by a
factor of about 80 on my machine, and your results, on your various home
machines will be different, but in the same ballpark.
import timeit
import numpy as np
py_sec = timeit.timeit('sum(x*x for x in range(1000))',
number=10000)
np_sec = timeit.timeit('na.dot(na)',
setup="import numpy as np; na=np.arange(1000)",
number=10000)
print(f"Normal Python: {py_sec:5.2f} sec")
print(f"NumPy: {np_sec:5.2f} sec")
Normal Python: 0.65 sec
NumPy: 0.01 sec
Note that numpy arrays in and of themselves don’t help. In the code
snippet below, we use elementwise arithmetic to multiply the na
array times itself and sum the result. This code takes around the same
amount of time as the basic Python code, because it doesn’t use the
proper optimized operation.
naive_np_sec = timeit.timeit('sum(na*na)',
setup="import numpy as np; na=np.arange(1000)",
number=10000)
print(("Naive NumPy: %f sec" % naive_np_sec))
Naive NumPy: 0.647754 sec
For example, simply changing from the builtin sum function to the
sum method helps enormously:
better_np_sec = timeit.timeit('(na*na).sum()',
setup="import numpy as np; na=np.arange(1000)",
number=10000)
print(("Better NumPy: %f sec" % better_np_sec))
Better NumPy: 0.040649 sec
Or almost as good, use numpy sum instead
better_np_sec = timeit.timeit('np.sum(na*na)',
setup="import numpy as np; na=np.arange(1000)",
number=10000)
print(("Better NumPy: %f sec" % better_np_sec))
Better NumPy: 0.058753 sec
The lesson here is that coding so as to take maximum advantage of the
efficiencies of numpy can be tricky, but if you have a good reason
to be efficient, it’s definitely worth some experimentation. That starts
with knowing about the kinds of builtin array specific functions
numpy offers.
A somewhat simpler example.
import random
import numpy as np
n = 1_000_000
x = [random.random() for _ in range(n)]
y = [random.random() for _ in range(n)]
xa = np.array(x)
ya = np.array(y)
Python list comprehension performing subtraction and the absolute value
operation on numbers that are values in Python lists x and y.
%timeit [abs(x[i] - y[j]) \
for i in range(1000) \
for j in range(1000)]
121 ms ± 831 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Vectorized abs on a numpy array resulting from elementwise
subtraction. Equivalent to previous calculation.
%timeit np.abs(xa[:1000, np.newaxis] - ya[:1000])
888 µs ± 3.96 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Since 121 ms is 121,000 µs, we have a speedup of 2 orders of magnitude.
121_000/888
136.26126126126127
