5.9. Putting it all together¶
In this section we deal withe xamples that combine some of the concepts we’ve been discussing int complete functions or programs.
5.9.1. Example One: Word counting¶
The following code puts a lot of the concepts we have been using together.
Let’s assume we want a program, that does the following: It opens up a text file and counts the words in the file and prints out the 10 most common words. Let’s say we want to call the program like this:
% python count_words.py pride_and_preudice.txt
Where pride_and_prejudice.txt is the name
of the file we want to count the words of.
Then we create a python file name count_words.py and
we out the following code into it.:
1from collections import Counter
2import sys
3
4def word_freqs(filename):
5 freqdist = Counter()
6 ## Read in the file
7 filehandle = open(filename, 'r')
8 ## Loop through each line and in each line loop
9 ## through each word
10 for line in filehandle:
11 line_list = line.split()
12 for word in line_list:
13 ## tabulate all words counts
14 freqdist[word] += 1
15 print freq_dist.most_common(10)
16 return freqdist
17
18
19 if __name__ == '__main__':
20 if len(sys.argv) == 2:
21 filename = sys.argv[1]
22 word_freqs(filename)
Covering this line by line:
We import a new module
collectionsto makeCountersavailable.
We create a counter
We open the file
We loop through it line by line
We split the current line into a list of words
We loop through the wordsin the current line
We update the count of the current word by one
Having exited the loop (look at indentation), we print out some information from the counter
We return the counter
We enter the part of the program that will be executed each time the file is loaded as a top level module in Python (it isn’t being imported by some other program).
In that case there will be a list of command line arguments (all strings) in
sys.argv. The first is the program name. The second is the filename the user supplied when calling the program. We set the variablefilenameto the second commandline argument.We call the function
word_freqsonfilename. It counts the word frequencies and prints out the top 10 words.That’s all. The script (and Python) will now be exited.
5.9.2. Example two: precision and recall¶
Let’s use what we know about Booleans to perform a simple data analysis task.
Suppose we have a system that predicts something, say, whether it will be sunny today, and let’s furthermore assume that we assembled a list of such predictions, together with the actual outcome of what was predicted. When the prediction and the outcome are the same, we have a successful prediction. When they differ, we have a failed prediction. So:
data = [('sunny','sunny'), ('sunny','cloudy'), ('sunny', 'rainy'), ('rainy','rainy')]
records a sequence of predictions in which two out of four are failures.
Three important scores for evaluating our performance are called accuracy, precision, and recall. For the above data, assuming that the task is predicting sunny days, we’ll call a ‘sunny’ day ‘positive’ and anything else ‘negative’, Putting all our system’s positive predictions in the first row and all the negative predictions in the second, we can tabulate our prediction success with a contingency table as follows:
Pred/Outcome |
Pos |
Neg |
|---|---|---|
Pos |
1 |
0 |
tp |
fn |
|
Neg |
2 |
1 |
fp |
tn |
Let N be the size of the dataset, 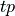 and
and  be true and
false positive respectively and
be true and
false positive respectively and 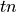 and
and 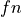 be true and
false negatives respective.
Accuracy is the percentage of correct
answers out of the total dataset
be true and
false negatives respective.
Accuracy is the percentage of correct
answers out of the total dataset 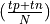 .
In this case the total dataset has size 4, 2 are correctly
classified, so the accuracy is .5. Precision is
the percentage of true positives out all positive guesses the system made
.
In this case the total dataset has size 4, 2 are correctly
classified, so the accuracy is .5. Precision is
the percentage of true positives out all positive guesses the system made
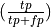 , so in this case
precision is .33. Recall is the percentage of true
positives out of actual positives
, so in this case
precision is .33. Recall is the percentage of true
positives out of actual positives 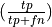 .
In this case there was one actually sunny day out of the 4,
and we predicted it, so is recall is 1.0.
.
In this case there was one actually sunny day out of the 4,
and we predicted it, so is recall is 1.0.
1def do_evaluation (pairs, pos_cls='pos'):
2 (N, tp, tn, fp,fn) = (0,0,0,0,0)
3 for (predicted, actual) in pairs:
4 N += 1
5 if predicted == actual:
6 if actual == pos_cls:
7 tp += 1
8 else:
9 tn += 1
10 else:
11 if actual == pos_cls:
12 fn += 1
13 else:
14 fp += 1
15 (accuracy, precision, recall) = (float(tp + tn)/N,float(tp)/(tp + fp),float(tp)/(tp + fn))
16 return (accuracy, precision, recall)
Considering this line by line:
Two arguments to the function, we’ll call the default positive class (the one whose presence we’re testing for)
'pos'
We set a number of variables in one line by assigning to a tuple of variables. We have to keep counts of the 4 cells in the contingency table, as well as the total number of things.
Notice the indentation is crucial . The
elseon line 10 has to belong to theifon line 8, not to theifon line 6, and the indentation shows that.
Again, the indentation is crucial . The
elseon line 12 belongs to theifon line 6, not to theifon line 8, and the indentation shows that.
To do our evaluation, we would do:
>>> data = [('sunny','sunny'), ('sunny','cloudy'), ('sunny', 'rainy'), ('rainy','rainy')]
>>> (acc,pre, rec) = do_evaluation(data,pos_cls= 'sunny')
>>> print 'Acc: {0:.2f} Prec: {1:.2f} Rec: {2:.2f}'.format(acc,pre,rec)
Acc: 0.50 Prec: 0.33 Rec: 1.00
