|
|
The grammar and lexicon:
pp -> p np vpg -> vbg np X2 -> X1 pp vp -> vbz np vp -> X1 pp vp -> X2 pp ap -> rb a s -> np vp np -> dt nbar np -> X3 np np -> ap nbar np -> nbar pp np -> n n np -> vbg np X3 -> np cc X1 -> vbz np nbar -> ap nbar nbar -> nbar pp nbar -> n n nbar -> vbg np
a: dt and: cc use: n np nbar codes: n np nbar sees: vbz of: p agency: n np nbar rapidly: rb handling: vbg labor: n np nbar volume: n np nbar as: p costs: n np nbar controlling: vbg way: n np nbar growing: a ap mail: n np nbar the: dt widespread: a ap
Your task was to explain the entries in the last column of the chart, which included all entries ending at index 10.
The modified chart below contains explanations for all the edges, lexical and non lexical. The lexical edges are for all spans of length 1, so the only ones you were responsible for in the assignment were those in cell (9,10).
np -> dt nbar
You can report your discovery of a rule edge in a simple format called a dtr record. Just give cat, the span, cat1 and cat2, and the value of k. So for our example, this is:
np (8,10) (det,9,nbar)
Finally, this sentence has 5 parses in this grammar. This is because certain edges contributing to the s edge in the (0,10) cell can be built in more than one way, given the grammar. These are called ambiguous edges. Find these ambiguous edges. They may not be in the last column, but they are in the chart, Give the lexical records or daughter records for these edges. You do not have to find all the ambiguous edges, just the ones contributing to the final 5 parses. Finally you do not have to find all the edges contributing to the final 5 parses, just the ambiguous ones.
There are 27 edges in red below. These are the only edges to contributed to some parse of the example sentence.
|
|
The explanation for why the sentence has 5 parses is contained in the last column.
Although S(0,10) can only be built one way, it is built out of np(0,2) and vp(2,10), and vp(2,10) can be built 4 ways:
VP(2, 10) --------------- 1. (vbz,3,np) 2. (X1, 4, pp) 3. (X2,7,pp) 4. (X1, 7,pp)
np(3, 10) --------------- 1. (nbar, 4, pp) 2. (nbar, 7, pp)
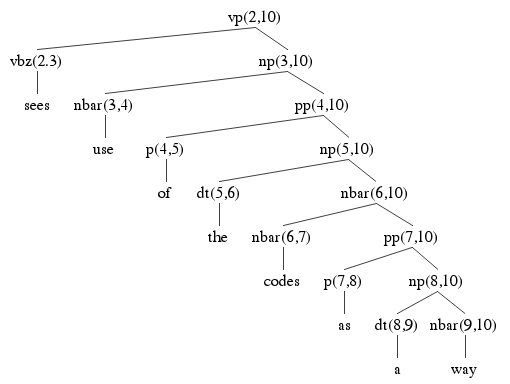
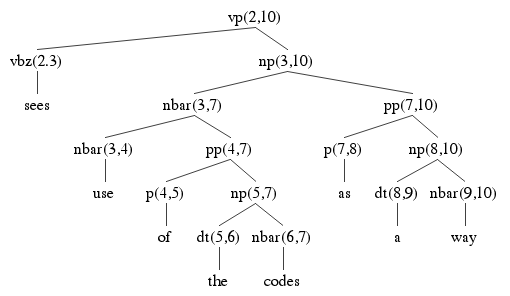
Here are the two parse trees using the ambiguous np from 3 to 10, each using a different way of building it. Check the answer key above to make sure where each of the nodes in the parse tree is coming from. Each node is labeled with its start and end indices, to help find it in the table above. You should also verify that each tree obeys the rules of the grammar. Notice how many edges are shared between the parse trees. They all use pp(7,10). Two of them use PP(4,10). Two of them use X1(2,4), and so on. This is the key to how an exponential number of parse trees can be used using only n2 memory.
Each parse tree has 15 nodes. That's 5 * 15 = 75 nodes. That's 75 parse tree nodes built using 27 chart edges, so that's quite a lot of re-use.

|

|
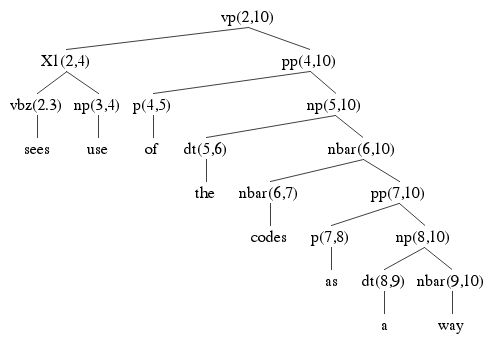
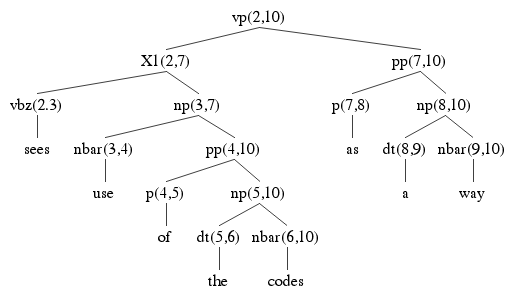
Here are the remaining three parses:
|

|
|
Finally, you should try to determine which of the parse trees is the correct one. The question is made more difficult by the fact that the original grammar has been distorted by the Chomsky Normal Form transformation. Remember the category names beginning with X have been introduced by the transformation to split a rule that introduced more than two categories. So:
VP → VBZ NP PP
VP → X1 PP X1 → VBZ NP