CKY Assignment
Below we give the CKY chart for a parse of the 10-word sentence:
The agency sees use of the codes as a way.
The assignment is to explain some features of the chart
resulting from use of the CKY algorithm to parse
this sentence.
We first give the grammar the parser uses (in Chomsky Normal Form), as well as the lexicon.
Grammar
pp -> p np
vpg -> vbg np
X2 -> X1 pp
vp -> vbz np
vp -> X1 pp
vp -> X2 pp
ap -> rb a
s -> np vp
np -> dt nbar
np -> X3 np
np -> ap nbar
np -> nbar pp
np -> n n
np -> vbg np
X3 -> np cc
X1 -> vbz np
nbar -> ap nbar
nbar -> nbar pp
nbar -> n n
nbar -> vbg np
Lexicon
a: dt
and: cc
use: n np nbar
codes: n np nbar
sees: vbz
of: p
agency: n np nbar
rapidly: rb
handling: vbg
labor: n np nbar
volume: n np nbar
as: p
costs: n np nbar
controlling: vbg
way: n np nbar
growing: a ap
mail: n np nbar
the: dt
widespread: a ap
Part A: Understanding chart edges
Your task concerns only the entries in the last column of the
chart, which includes all entries
ending at index 10. In "chart parsing" speak. These entries are referred
to as edges.
Basically there are two kinds of edges
in the chart.
| Lexical Edges |
For example there is an entry associating way
with the category n in the lexicon above,
and there is an entry for an n in the (9,10)
cell of the chart below.
|
You can report a lexical edge
in a format known as a lexical record.
Just report the word, the span, and the
category:
Lexical edge
way (9,10) n
|
|
Daughter
Edges
|
For example, there is an entry for np in the (8,10)
cell of the chart below, and this is explained by the fact
that there is a rule in the
grammar.
np -> dt nbar
and there is a dt in the (8,9) cell of the chart
and an nbar in the (9,10) cell.
|
You can report a rule edge
in a simple format called a dtr record. Just give cat,
the span, cat1 and cat2, and the
value of k. So for our example, this is:
np (8,10)
(det,9,nbar)
|
Part B: Finding ambiguous edges
Finally, this sentence has 5 parses in this grammar.
This is because certain edges contributing to the
s edge in the (0,10) cell can be built in more than one way, given
the grammar. These are called
ambiguous edges. Find these ambiguous
edges. They may not be in the last
column, but they are in the chart,
Give the lexical records or daughter records for these
edges. You do not have to find all the ambiguous
edges, just the ones contributing to the final 5 parses.
Finally you do not have to find all the edges contributing
to the final 5 parses, just the ambiguous ones.
When you have found the ambiguous edges, you are ready to draw the five
parse trees that this chart contains. Each parse tree starts
with the edge S(0,10). Each will continue with the dtr record or
records you found for that S. Each daughter record will lead you to
two other edges that are daughters for that S.
Ambiguous edges (with more than one daughter record) will generate
more than one parse tree. But just because an edge is not ambiguous
does not mean it has only one parse tree. It may be ambiguous not because
it has more than one daughter record, but because one or more of its
daughters does. You should be able to build five parse trees in
this manner.
For example, the s(0,10) edge will have a daughter record (np,2,vp),
which leads to an np edge np(0,2) and a vp edge vp(2,10).
Continuing from those edges,
one of your five parse trees should look like this.
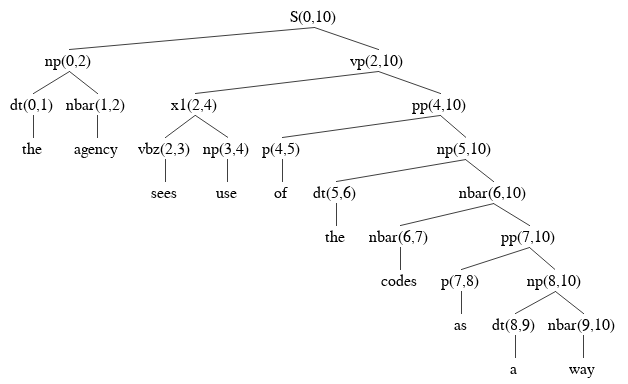
After you have drawn the addiitonal four parse trees,
you should indicate which one is the correct parse.
| |
(0, 1)
the |
(1, 2)
agency |
(2, 3)
sees |
(3, 4)
use |
(4, 5)
of |
(5, 6)
the |
(6, 7)
codes |
(7, 8)
as |
(8, 9)
a |
(9, 10)
way |
| j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| i |
| 0 | dt
| np
| | s
| | | s
| | | s
|
| 1 | | np
nbar
n
| | s
| | | s
| | | s
|
| 2 | | | vbz
| vp
X1
| | | vp
X2
X1
| | | vp
X2
X1
|
| 3 | | | | np
nbar
n
| | | np
nbar
| | | np
nbar
|
| 4 | | | | | p
| | pp
| | | pp
|
| 5 | | | | | | dt
| np
| | | np
|
| 6 | | | | | | | np
nbar
n
| | | np
nbar
|
| 7 | | | | | | | | p
| | pp
|
| 8 | | | | | | | | | dt
| np
|
| 9 | | | | | | | | | | np
nbar
n
|
Part C: Probabilities
Below we give the CKY chart for a parse of the 10-word sentence:
The agency sees use of the codes as a way.
The assignment is to assign probabilities to each of the edges
used in the 5 parses the example sentence has using
the probabilities in the Probabilistic CF grammar
below. You do not have to assign probabilities to
edges not used in any of the 5 parses. You will find it helpful
to use the solution to the last
assignment as a guide to make sure you are
considering all possible ways of building each edge.
What you need to hand in (a) the correct parse (in the form of a
tree like the one above) as selected by
the calculation of the Viterbi probability;
(b) a version of the chart below that has the Viterbi
values for each edge in the chart
that is used in one of the 5 parses;
(c) your calculations.
For example, your answer to (a) might be the parse tree
shown above, if that is indeed the winning parse
from among the five parses this sentence has.
Your answer to (b) for a four word sentence chart might look like
the chart below, using the grammar below:
| |
(0, 1)
the |
(1, 2)
agency |
(2, 3)
sees |
(3, 4)
codes |
| j |
1 |
2 |
3 |
4 |
| i |
| 0 | dt, .5
| np, .0025
| | s, .00001 |
| 1 |
| n, .01
nbar, .01
| | |
| 2 |
|
|
vbz, 1.0 |
vp, .004 |
| 3 |
|
| |
n, .01
nbar, .01 |
Finally, your answer to (c) will require showing the Parse probability
calculation for each edge used in a parse. Each daughter record gives
rise to a path probability. The Viterbi probability for an edge
is the maximum of all the path probabilities. And the winning
daughter record for that edge is the daughter record that gave rise
to that maximum. So for example, inspection of the chart above shows
that the edge s(0,4) has only one daughter record (np,2,vp). So
we need to compute the path probability for that daughter record:
path_prob(s(0,10), np(0,2), vp(2,4)) =
Vit(np(0,2)) * Vit(vp(2,4)) * Rule_prob(s → np vp)
That is the path probability is the Viterbi probability of the
np edge (Vit(np(0,2))) times the viterbi probability of the vp edge
(Vit(vp(2,4)))
times the rule probability. Looking those up in the chart and the grammar, we have:
path_prob(s(0,10), np(0,2), vp(2,4)) =
.0025 * .004 * 1.0 = .00001
And the Viterbi value of the edge is the max of all the path
probabilities. This edge has only one daughter record (it's
not an ambiguous edge), so it has
onlt one path-prob, so its maximization step looks like this:
Vit(s(0,4)) = max { path_prob(s(0,10), np(0,2), vp(2,4)) } = .00001
We first give the grammar the parser uses (in Chomsky Normal Form), as well as the lexicon.
Probabilistic Context Free Grammar
pp -> p np, 1.0
vpg -> vbg np, 1.0
X2 -> X1 pp, 1.0
vp -> vbz np, .4
vp -> X1 pp, .5
vp -> X2 pp, .1
ap -> rb a, 1.0
s -> np vp, 1.0
np -> dt nbar, .5
np -> X3 np, .1
np -> ap nbar, .05
np -> nbar pp, .2
np -> n n, .05
np -> vbg np, .05
X3 -> np cc, 1.0
X1 -> vbz np, 1.0
nbar -> ap nbar, .1
nbar -> nbar pp, .3
nbar -> n n, .5
nbar -> vbg np, ..05
Lexicon
a: dt, .5
and: cc, 1.0
use: n,.01; np,01; nbar.01
codes: n,.01; np,01; nbar,.01
sees: vbz,1.0
of: p,.5
agency: n,.01; np,.01; nbar,.01
rapidly: rb,1.0
handling: vbg,.5
labor: n,.01; np,.01, nbar
as: p,.5
costs: n,.01; np,.01 nbar,.01
controlling: vbg,.5
way: n,.01; np,.01; nbar,.01
growing: a,.5 ap,.5
the: dt,.5
widespread: a,5, ap,5
| |
(0, 1)
the |
(1, 2)
agency |
(2, 3)
sees |
(3, 4)
use |
(4, 5)
of |
(5, 6)
the |
(6, 7)
codes |
(7, 8)
as |
(8, 9)
a |
(9, 10)
way |
| j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| i |
| 0 | dt
| np
| | s
| | | s
| | | s
|
| 1 | | np
nbar
n
| | s
| | | s
| | | s
|
| 2 | | | vbz
| vp
X1
| | | vp
X2
X1
| | | vp
X2
X1
|
| 3 | | | | np
nbar
n
| | | np
nbar
| | | np
nbar
|
| 4 | | | | | p
| | pp
| | | pp
|
| 5 | | | | | | dt
| np
| | | np
|
| 6 | | | | | | | np
nbar
n
| | | np
nbar
|
| 7 | | | | | | | | p
| | pp
|
| 8 | | | | | | | | | dt
| np
|
| 9 | | | | | | | | | | np
nbar
n
|
